СПРАВОЧНЫЕ МАТЕРИАЛЫ
Некоторые неопределённые и несобственные интегралы и некоторые формулы.
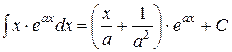
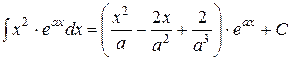
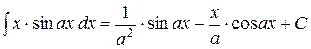
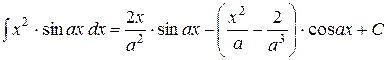

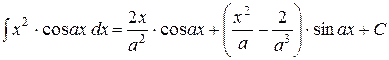

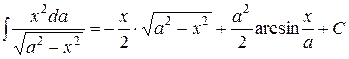
 ; ; 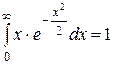 ; ; 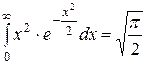
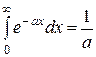 ; ; 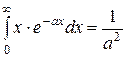 ; ; 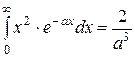 ; ; 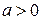
Формула Стирлинга: 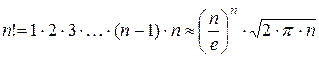
Размещения сочетания (из n элементов по m) и перестановки (из n элементов):
 ; ; 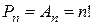
 ; ; 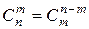
Примечание: если при определении функции y(x) соответствующего значения аргумента в приведенных таблицах нет, следует воспользоваться линейной интерполяцией, вычисляя её по следующей формуле:
где xi и xi+1 ближайшие к x (xi < x < xi + 1) табличные значения.
Таблица 1. Значения функции 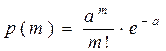
| a\m
|
|
|
|
|
|
|
|
| | 0,1
| 00,90484
|
|
|
|
|
|
|
| | 0,2
|
|
|
|
|
|
|
|
| | 0,3
|
|
|
|
|
|
|
|
| | 0,4
|
|
|
|
|
|
|
|
| | 0,5
|
|
|
|
|
|
|
|
| | 0,6
|
|
|
|
|
|
|
|
| | 0,7
|
|
|
|
|
|
|
|
| | 0,8
|
|
|
|
|
|
|
|
| | 0,9
|
|
|
|
|
|
|
|
| | 1,0
|
|
|
|
|
|
|
|
| | 2,0
|
|
|
|
|
|
|
|
| | 3,0
|
|
|
|
|
|
|
|
| | 4,0
|
|
|
|
|
|
|
|
| | 5,0
|
|
|
|
|
|
|
|
| | 6,0
|
|
|
|
|
|
|
|
| | 7,0
|
|
|
|
|
|
|
|
| Таблица 2. Значения функции 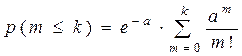
| a\k
|
|
|
|
|
|
|
|
| | 0,1
| 0,90484
|
|
| 1,000
| 1,000
| 1,000
| 1,000
| 1,000
| | 0,2
|
|
|
|
| 1,000
| 1,000
| 1,000
| 1,000
| | 0,3
|
|
|
|
|
| 1,000
| 1,000
| 1,000
| | 0,4
|
|
|
|
|
| 1,000
| 1,000
| 1,000
| | 0,5
|
|
|
|
|
|
| 1,000
| 1,000
| | 0,6
|
|
|
|
|
|
| 1,000
| 1,000
| | 0,7
|
|
|
|
|
|
|
| 1,000
| | 0,8
|
|
|
|
|
|
|
| 1,000
| | 0,9
|
|
|
|
|
|
|
| 1,000
| | 1,0
|
|
|
|
|
|
|
|
| | 2,0
|
|
|
|
|
|
|
|
| | 3,0
|
|
|
|
|
|
|
|
| | 4,0
|
|
|
|
|
|
|
|
| | 5,0
|
|
|
|
|
|
|
|
| | 6,0
|
|
|
|
|
|
|
|
| | 7,0
|
|
|
|
|
|
|
|
| Таблица 3. Значения функции 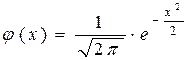
| x
|
|
|
|
|
|
|
|
|
|
| | 0,0
| 0,3989
|
|
|
|
|
|
|
|
|
| | 0,1
|
|
|
|
|
|
|
|
|
|
| | 0,2
|
|
|
|
|
|
|
|
|
|
| | 0,3
|
|
|
|
|
|
|
|
|
|
| | 0,4
|
|
|
|
|
|
|
|
|
|
| | 0,5
|
|
|
|
|
|
|
|
|
|
| | 0,6
|
|
|
|
|
|
|
|
|
|
| | 0,7
|
|
|
|
|
|
|
|
|
|
| | 0,8
|
|
|
|
|
|
|
|
|
|
| | 0,9
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| | 1,0
|
|
|
|
|
|
|
|
|
|
| | 1,1
|
|
|
|
|
|
|
|
|
|
| | 1,2
|
|
|
|
|
|
|
|
|
|
| | 1,3
|
|
|
|
|
|
|
|
|
|
| | 1,4
|
|
|
|
|
|
|
|
|
|
| | 1,5
|
|
|
|
|
|
|
|
|
|
| | 1,6
|
|
|
|
|
|
|
|
|
|
| | 1,7
|
|
|
|
|
|
|
|
|
|
| | 1,8
|
|
|
|
|
|
|
|
|
|
| | 1,9
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| | 2,0
|
|
|
|
|
|
|
|
|
|
| | 2,1
|
|
|
|
|
|
|
|
|
|
| | 2,2
|
|
|
|
|
|
|
|
|
|
| | 2,3
|
|
|
|
|
|
|
|
|
|
| | 2,4
|
|
|
|
|
|
|
|
|
|
| | 2,5
|
|
|
|
|
|
|
|
|
|
| | 2,6
|
|
|
|
|
|
|
|
|
|
| | 2,7
|
|
|
|
|
|
|
|
|
|
| | 2,8
|
|
|
|
|
|
|
|
|
|
| | 2,9
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| | 3,0
|
|
|
|
|
|
|
|
|
|
| | 3,1
|
|
|
|
|
|
|
|
|
|
| | 3,2
|
|
|
|
|
|
|
|
|
|
| | 3,3
|
|
|
|
|
|
|
|
|
|
| | 3,4
|
|
|
|
|
|
|
|
|
|
| | 3,5
|
|
|
|
|
|
|
|
|
|
| Таблица 4. Значения функции 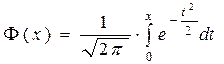 . .
| x
|
|
|
|
|
|
|
|
|
|
| | 0,0
| 00,0000
|
|
|
|
|
|
|
|
|
| | 0,1
|
|
|
|
|
|
|
|
|
|
| | 0,2
|
|
|
|
|
|
|
|
|
|
| | 0,3
|
|
|
|
|
|
|
|
|
|
| | 0,4
|
|
|
|
|
|
|
|
|
|
| | 0,5
|
|
|
|
|
|
|
|
|
|
| | 0,6
|
|
|
|
|
|
|
|
|
|
| | 0,7
|
|
|
|
|
|
|
|
|
|
| | 0,8
|
|
|
|
|
|
|
|
|
|
| | 0,9
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| | 1,0
|
|
|
|
|
|
|
|
|
|
| | 1,1
|
|
|
|
|
|
|
|
|
|
| | 1,2
|
|
|
|
|
|
|
|
|
|
| | 1,3
|
|
|
|
|
|
|
|
|
|
| | 1,4
|
|
|
|
|
|
|
|
|
|
| | 1,5
|
|
|
|
|
|
|
|
|
|
| | 1,6
|
|
|
|
|
|
|
|
|
|
| | 1,7
|
|
|
|
|
|
|
|
|
|
| | 1,8
|
|
|
|
|
|
|
|
|
|
| | 1,9
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| | 2,0
|
|
|
|
|
|
|
|
|
|
| | 2,1
|
|
|
|
|
|
|
|
|
|
| | 2,2
|
|
|
|
|
|
|
|
|
|
| | 2,3
|
|
|
|
|
|
|
|
|
|
| | 2,4
|
|
|
|
|
|
|
|
|
|
| | 2,5
|
|
|
|
|
|
|
|
|
|
| | 2,6
|
|
|
|
|
|
|
|
|
|
| | 2,7
|
|
|
|
|
|
|
|
|
|
| | 2,8
|
|
|
|
|
|
|
|
|
|
| | 2,9
|
|
|
|
|
|
|
|
|
|
|
| x
|
| x
|
| x
|
| x
|
| | 3,0
| 0,49865
| 3,5
| 0,49977
| 4,0
| 0,499968
| 4,5
| 0,4999966
| | 3,1
|
| 3,6
|
| 4,1
|
| 4,6
|
| | 3,2
|
| 3,7
|
| 4,2
|
| 4,7
|
| | 3,3
|
| 3,8
|
| 4,3
|
| 4,8
|
| | 3,4
|
| 3,9
|
| 4,4
|
| 4,9
|
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
ТЕОРИЯ ЗАЩИТНЫХ МЕХАНИЗМОВ ЛИЧНОСТИ В современной психологической литературе встречаются различные термины, касающиеся феноменов защиты...
Этические проблемы проведения экспериментов на человеке и животных В настоящее время четко определены новые подходы и требования к биомедицинским исследованиям...
Классификация потерь населения в очагах поражения в военное время Ядерное, химическое и бактериологическое (биологическое) оружие является оружием массового поражения...
|
Педагогическая структура процесса социализации Характеризуя социализацию как педагогический процессе, следует рассмотреть ее основные компоненты: цель, содержание, средства, функции субъекта и объекта...
Типовые ситуационные задачи. Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической
Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической нагрузке. Из медицинской книжки установлено, что он страдает врожденным пороком сердца....
Типовые ситуационные задачи. Задача 1.У больного А., 20 лет, с детства отмечается повышенное АД, уровень которого в настоящее время составляет 180-200/110-120 мм рт Задача 1.У больного А., 20 лет, с детства отмечается повышенное АД, уровень которого в настоящее время составляет 180-200/110-120 мм рт. ст. Влияние психоэмоциональных факторов отсутствует. Колебаний АД практически нет. Головной боли нет. Нормализовать...
|
|

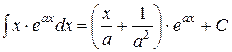
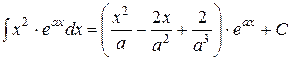
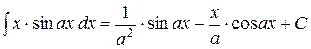
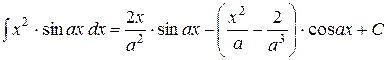

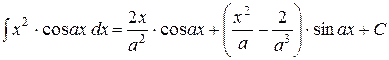

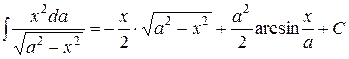
 ;
; 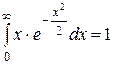 ;
; 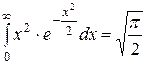
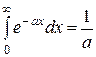 ;
; 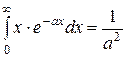 ;
; 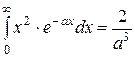 ;
; 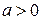
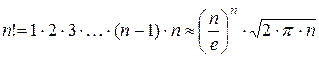
 ;
; 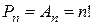
 ;
; 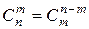
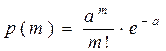
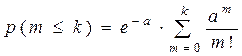
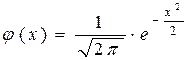
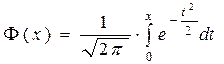 .
.


