Недостатком исследования газовых скважин при выполнении закона Дарси является то, что обработки подвергаются не все точки, а только те, которые ложатся на прямую линию при малых дебитах. Остальные точки отбрасываются, поэтому теряется информация и точность определения параметров пласта уменьшается.
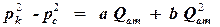 . .
| (3.40)
|
Эта линия представляет собой параболу. Для обработки результатов удобнее всего линейные зависимости. Преобразуем последнее уравнение к новым координатам таким образом, чтобы в новых координатах зависимость была линейной. Это можно сделать различными способами, но наиболее простой заключается в делении полученного уравнения на Qат. Тогда в новых координатах
 , ,
| (3.41)
|
теоретическая зависимость преобразуется в прямую линию
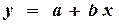
| (3.42)
|
Поэтому экспериментальные точки обрабатывают в этих координатах. По точкам графически или методом наименьших квадратов проводят прямую линию. Коэффициент “a этой линии представляет собой отрезок, отсекаемый линией на оси ординат (y). Коэффициент “b” — тангенс угла наклона прямой к оси абсцисс, b = tg α (рис. 3.5). Для того, чтобы найти этот коэффициент, необходимо на прямой выбрать какую – либо точку (*) и снять координаты этой точки y* и x*. Тогда значение коэффициента “b” будет равно
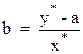 . .
| (3.43)
|
По известному значению коэффициента “ a ” находится гидропроводность пласта
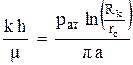 . .
| (3.44)
|
По коэффициенту “ b ” можно найти константу β;, которая входит в двухчленный закон фильтрации. Но обычно ее не определяют, а используют в дальнейшем само значение коэффициента “ b ”.

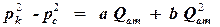 .
.
 ,
,
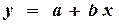
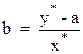 .
.
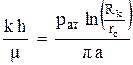 .
.



