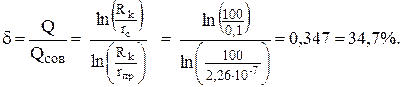Пример 2.6.
Пласт толщиной h = 12 м разрабатывается скважиной радиусом rc = 0,1 м и вскрывающей пласт на b = 3 м. Давления на контуре питания и скважине равны pк = 42 МПа и pс = 33 МПа. Пласт имеет проницаемость k = 170·10-15 м2. По пласту фильтруется нефть с коэффициентом динамической вязкости μ = 14 мПа·с и плотностью. Радиус контура питания находится на расстоянии Rk = 100 м. Скважина Несовершенна по характеру вскрытия. Глубина проникновения перфорационного канала в породу lп = 2 см, диаметр перфорационного канала dп = 1 см, число перфорационных отверстий на один метр длины скважины nп = 10 отв/м. Определить: коэффициенты учитывающие несовершенства скважины; приведенный радиус скважины; дебит скважины; коэффициент совершенства скважины.. Решение: По условиям задачи скважина является одновременно несовершенной и по степени и по характеру вскрытия. Для учета несовершенства по степени вскрытия пласта найдем отношение толщины скважины к диаметру скважины: h/Dc = 12/0,2 = 60 и относительное вскрытие пласта
По графику Шурова для нахождения C1 (см. рис. П 7.1) выбираем ближайшую линию к найденому значению h/Dc = 60. Ближайшая линия №6 имеет значение 80. На оси абцисс выбираем вычисленное значение относительного вскрытия пласта Для учета несовершенства по характеру вскрытия пласта найдем отношение глубины проникновения перфорационного канала в породу к диаметру скважины lп/Dc = 0,02/0,2 = 0,1; отношение диаметра перфорационного канала к диаметру скважины dп/Dc = 0,01/0,2 = 0,05; произведение число перфорационных отверстий на один метр длины скважины на диаметр скважины nп Dc= 10·0,2 = 2. По графикам Шурова для нахождения C2 (см. рис. П 7.2-П 7.6) выбираем график с ближайшую значением lп/Dc к найденому значению. В данном случае это график со значением lп/Dc = 0,1. По значению dп/Dc выбираем номер линии на графике. Значение dп/Dc = 0,05 лежит между линиями №2 и №3. На оси абцисс выбираем вычисленное значение nп Dc = 2 и ведем до пересечения с выбранной линией, а потом на шкалу значений С2. По графику находим C2 = 7,5. Приведенном радиусе скважины rпр рассчитаем по формуле: rпр = rc exp(-(С1 + С2)) = 0,1·exp(-(5,5 + 7,5)) = 0,1·exp(-13) = 2,26·10-7 м. Дебит несовершенной скважины рассчитаем по формуле:
Ответ: C1 = 5,5; C2 = 7,5; rпр = 2,26·10-7 м; Q = 4,14 10-4 м3/с; δ = 0,347. Задача 2.1 Определить значение числа Рейнольдса у стенки гидродинамически несовершенной по характеру вскрытия нефтяной скважины если известно, что эксплуатационная колонна перфорирована, на каждом погонном метре колонны прострелено 10 отверстий диаметром dп = 10 мм, толщина пласта h = 15 м, проницаемость пласта k = мкм2, пористость его m = 18%, коэффициент вязкости нефти μ = 4 мПа·с, плотность нефти ρ = 870 кг/м3 и дебит скважины составляет 140 м3/сут. Задача 2.2 Определить дебит галереи шириной В = 100 м, если толщина пласта h = 10 м, расстояние до контура питания L = 300 м, коэффициент проницаемости пласта k = 1 мкм2, динамический коэффициент вязкости нефти μ = 2 мПа·с, давление на контуре питания pк = 8 МПа и давление в галерее pг = 4 МПа. Задача 2.3 Определить нарушается ли закон Дарси в галереи шириной В = 200 м, если толщина пласта h = 5 м, расстояние до контура питания L = 100 м, коэффициент проницаемости пласта k = 0,2 мкм2, динамический коэффициент вязкости нефти μ = 2 мПа·с, пористость пласта 15%, давление на контуре питания pк = 18 МПа и давление в галерее pг = 4 МПа. Задача 2.4 Определить время движения нефти от контура питания к галереи шириной В = 200 м, если толщина пласта h = 15 м, расстояние до контура питания L = 200 м, коэффициент проницаемости пласта k = 0,5 мкм2, динамический коэффициент вязкости нефти μ = 12 мПа·с, пористость пласта 12%, давление на контуре питания pк = 18 МПа и давление в галерее pг = 8 МПа. Задача 2.5 Определить давление на расстоянии 50 метров от галереи шириной В = 200 м, если толщина пласта h = 15 м, расстояние до контура питания L = 200 м, коэффициент проницаемости пласта k = 0,15 мкм2, динамический коэффициент вязкости нефти μ = 12 мПа·с, дебит галереи 200 м3/сут и давление в галерее pг = 8 МПа. Задача 2.6 Определить дебит нефтяной скважины в случае установившейся плоскорадиальной фильтрации нефти по закону Дарси, если известно, что давление на контуре питания pк = 18 МПа, давление на забое скважины pс = 10 МПа, коэффициент проницаемости пласта k = 0,3 мкм2, толщина пласта h = 15 м, диаметр скважины Dс = 20 см, радиус контура питания Rk = 1 км, динамический коэффициент вязкости нефти μ = 12 мПа·с. Задача 2.7 Определить нарушается ли закон Дарси на расстоянии 1 м от нефтяной скважины, если известно, что давление на контуре питания pк = 8 МПа, давление на забое скважины pс = 3 МПа, коэффициент проницаемости пласта k = 0,3 мкм2, толщина пласта h = 10 м, диаметр скважины Dс = 20 см, радиус контура питания Rk = 100 м, динамический коэффициент вязкости нефти μ = 20 мПа·с, пористость пласта 12%. Задача 2.8 Определить время движения нефти от контура питания к скважине, если известно, что давление на контуре питания pк = 15 МПа, давление на забое скважины pс = 5 МПа, коэффициент проницаемости пласта k = 0,6 мкм2, толщина пласта h = 5 м, диаметр скважины Dс = 20 см, радиус контура питания Rk = 100 м, динамический коэффициент вязкости нефти μ = 15 мПа·с, пористость пласта 17%. Задача 2.9 Определить давление на расстоянии 3 м от нефтяной скважины в случае установившейся плоскорадиальной фильтрации нефти по закону Дарси, если известно, что давление на контуре питания pк = 28 МПа, коэффициент проницаемости пласта k = 0,3 мкм2, толщина пласта h = 15 м, диаметр скважины Dс = 20 см, радиус контура питания Rk = 1 км, динамический коэффициент вязкости нефти μ = 12 мПа·с. Дебит нефтяной скважины 86 м3/сут. Задача 2.10 По модели пласта в виде керна диаметром 2 см и длиной 5 см за десять минут прокачано два литра нефти. Определить коэффициент проницаемости керна, если известно, что разность давлений на входе жидкости в образец и на выходе Δp = 1,2 МПа, динамический коэффициент вязкости нефти μ = 12 мПа·с. Задача 2.11 Построить индикаторную диаграмму для нефтяной совершенной скважины, если известно, что давление на контуре питания pk = 8,82 МПа, коэффициент проницаемости пласта k = 0,06 мкм2, толщина пласта h = 10 м, диаметр скважины Dс = 24,8 см, расстояние от оси скважины до контура питания Rk = 10 км и динамический коэффициент вязкости нефти μ = 5 мПа с. Фильтрации происходит по закону Дарси. Задача 2.12 Нефтяная скважина радиусом rc = 0,1 м и контуром питания Rk = 250 м дают дебит 100 м3/сут. Определить дебит скважины при той - же депрессии, если радиус скважины увеличить в два раза.
Задача 2.17 Определить дебит нефтяной галереи шириной В = 100 м, расстояние до контура питания L = 300 м, динамический коэффициент вязкости нефти μ = 2 мПа·с, давление на контуре питания pк = 8 МПа и давление на галерее pг = 4 МПа. Пласт неоднороден по толщине и состоит из трех пропластков проницаемость которых 0,25; 0,12 и 0,06 мкм2, а толщины 2; 3 и 5 метров. Задача 2.18 Определить дебит нефтяной галереи шириной В = 150 м, расстояние до контура питания L = 200 м, динамический коэффициент нефтяной нефти μ = 12 мПа·с, давление на контуре питания pк = 18 МПа и давление на галерее pг = 5 МПа. Пласт состоит из двух зон. Проницаемости первой и второй зоны соответственно равны 0,12 и 0,26 мкм2 Длина первой зоны 50 метров. Толщина пласта 5 м. Задача 2.19 Происходит приток нефти к галерее в зонально-неоднородном пласте. Пласт состоит из двух зон. Проницаемости первой и второй зоны соответственно равны 0,52 и 0,16 мкм2. Длинны зон 50 и 150 м. Определить давление на границе зон, если давление на контуре питания pк = 18 МПа и давление на галерее pг = 5 МПа. Задача 2.20 Определить дебит газовой галереи шириной В = 100 м, расстояние до контура питания L = 300 м, динамический коэффициент вязкости газа μ = 0,017 мПа·с, абсолютные давление на контуре питания pк = 10 МПа и давление на галерее pг = 5 МПа. Пласт неоднороден по толщине и состоит из трех пропластков проницаемость которых 0,20; 0,15 и 0,05 мкм2, а толщины 3; 2 и 5 метров. Задача 2.21 Определить дебит газовой галереи шириной В = 150 м, расстояние до контура питания L = 200 м, динамический коэффициент вязкости газа μ = 0,015 мПа·с, абсолютные давление на контуре питания pк = 18 МПа и давление на галерее pг = 8 МПа. Пласт состоит из двух зон. Проницаемости первой и второй зоны соответственно равны 0,26 и 0,12 мкм2 Длина первой зоны 50 метров. Толщина пласта 15 м Задача 2.22 Происходит приток газа к галерее в зонально-неоднородном пласте. Пласт состоит из двух зон. Проницаемости первой и второй зоны соответственно равны 0,25 и 0,10 мкм2 Длинны зон 100 и 150 м. Определить давление на границе зон, если абсолютные давление на контуре питания и галереи 20 и 5 МПа. Задача 2.23 Определить дебит нефтяной скважины с расстоянием до контура питания Rк = 300 м, динамический коэффициент вязкости нефти μ = 2 мПа·с, давление на контуре питания pк = 8 МПа и давление на скважине pс = 4 МПа. Пласт неоднороден по толщине и состоит из трех пропластков проницаемость которых 0,35; 0,22 и 0,16 мкм2, а толщины 2; 3 и 5 метров. Задача 2.24 Определить дебит нефтяной скважины с расстоянием до контура питания Rк = 200 м, динамический коэффициент вязкости жидкости μ = 12 мПа·с, давление на контуре питания pк = 18 МПа и давление на скважине pс = 5 МПа. Пласт состоит из двух зон. Проницаемости первой и второй зоны соответственно равны 0,12 и 0,5 мкм2 Внешние радиусы зон 1 и 100 метров. Толщина пласта 8 м Задача 2.25 Происходит приток нефти к скважине в зонально-неоднородном пласте. Пласт состоит из двух зон. Проницаемости первой и второй зоны соответственно равны 0,20 и 0,40 мкм2 Внешние радиусы зон 1 и 100 метров. Определить давление на границе зон, если давление на контуре питания pк = 25 МПа и давление на галерее pс = 5 МПа. Задача 2.26 Определить дебит газовой скважины с расстоянием до контура питания Rк = 200 м, динамический коэффициент вязкости газа μ = 0,015 мПа·с, давление на контуре питания pк = 9 МПа и давление на скважине pс = 4 МПа. Пласт неоднороден по толщине и состоит из трех пропластков проницаемость которых 0,15; 0,22 и 0,36 мкм2, а толщины 5; 3 и 2 метров. Задача 2.27 Определить дебит газовой скважины с расстоянием до контура питания Rк = 100 м, динамический коэффициент вязкости газа μ = 0,017 мПа·с, абсолютные давление на контуре питания pк = 17 МПа и давление на скважине pс = 8 МПа. Пласт состоит из двух зон. Проницаемости первой и второй зоны соответственно равны 0,25 и 0,40 мкм2 Внешний радиус первой зоны 1 м. Толщина пласта 9 м Задача 2.28 Происходит приток газа к скважины в зонально-неоднородном пласте. Пласт состоит из двух зон. Проницаемости первой и второй зоны соответственно равны 0,20 и 0,50 мкм2 Внешние радиусы зон 1 и 100 метров. Определить давление на границе зон, если абсолютные давление на контуре питания и галереи 20 и 5 МПа. Задача 2.29 В однородном нефтяном пласте с проницаемостью k провели соляно-кислотную обработку. После этого вокруг скважины образовались три зоны. В первой зоне радиусом 0,2 м проницаемость возросла в 10 раз, во второй зоне радиусом 1 м проницаемость возросла в 3 раза и третьей зоне радиусом 100 метров проницаемость не изменилась. Во сколько раз увеличится дебит скважины?
|

 = b/h = 3/12 = 0,4 = 40%.
= b/h = 3/12 = 0,4 = 40%.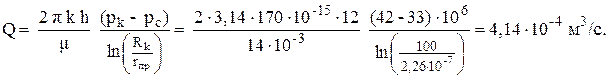 Коэффициентом совершенства скважины d называется отношение дебита несовершенной скважины к дебиту совершенной скважины
Коэффициентом совершенства скважины d называется отношение дебита несовершенной скважины к дебиту совершенной скважины