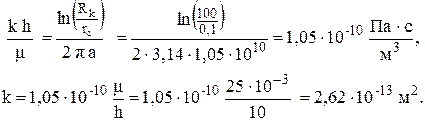Пример 2.3.
При исследовании нефтяной скважины на стационарном режиме получены следующие значения манометрических давлений и расходов, которые приведены в первых двух столбцах таблицы 2.1. Построить индикаторную диаграмму. Определить проницаемость пласта, если радиус контура питания 100 м, радиус скважины 0,1 м, толщина пласта 10 м, а вязкость нефти μ = 25 мПа·с. Решение:
Для построения индикаторной диаграммы найдем депрессию на скважине. Когда скважина не работает, то давление в горизонтальном пласте одинаково и равно давлению на контуре, то есть Pмk = Pмc0 = 49,9 МПа. Тогда депрессия для второй строчки данных равна Dp2 = pмс0 - pмс1 = 49,9 – 48,8 = 1,1 МПа. Аналогично рассчитаем остальные депрессии и занесем в третий столбец Таблицы 2.1 (расчетные значения выделены курсивом). По полученным данным строим индикаторную диаграмму. При фильтрации по закону Дарси, индикаторная диаграмма представляет собой прямую линию, выходящую из начала координат. Поэтому по точкам индикаторной диаграммы проводим прямую линию. На этой линии выбираем точку (*) и снимаем значения координат этой точки Dp* = 3,64 МПа, Q* = 30 м3/сут. Находим коэффициент продуктивности скважины К и коэффициент
фильтрационного сопротивления a: По значению фильтрационного сопротивления находим коэффициент гидропроводности пласта и проницаемость пласта:
Более точно параметры пласта можно найти обработав результаты исследования методом наименьших квадратов. Ответ: k = 2,62 10-13 м2.
|
. Обработка результатов исследования нефтяной скважины на стационарных режимах
