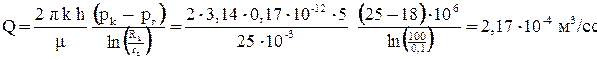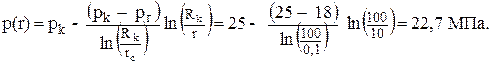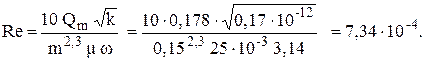Пример 2.2.

Пласт толщиной h = 5 м разрабатывается скважиной радиусом r_c = 0,1 м. Давления на контуре питания и скважине равны p_к = 25 МПа и p_с = 18 МПа. Пласт имеет проницаемость k = 0,17 мкм² и пористость m = 15%. По пласту фильтруется нефть с коэффициентом динамической вязкости μ = 25 мПа·с и плотностью ρ = 820 кг/м³. Радиус контура питания находится на расстоянии R_k = 100 м.

Определить:

дебит скважины;

давление на расстоянии 10 м от скважины;

время разработки нефти из скважины;

нарушается ли закон Дарси на боковой поверхности скважины?

Решение:

Дебит скважины при фильтрации нефти рассчитывается по формуле Дюпюи:

Давление в точке с координатами r = 10 м удобно рассчитывать по формуле:

При поршневом вытеснении время разработки скважины соответствует движению частицы нефти от контура питания к скважине. Поэтому координата частицы на момент окончания разработки равна r = r_c. Тогда время разработки равно:

 

Для того, чтобы определить выполняется ли закон Дарси необходимо рассчитать число Рейнольдса в данной точке. Число Рейнольдса удобно рассчитывать по формуле:

Массовый расход нефти Q_m = Q r = 2,17×10^-4 ×820 = 0,178 кг/с. Площадь поперечного сечения зависит от расстояния до скважины. Поэтому число Рейнольдса будет различным, на различных расстояниях от скважины. На боковой поверхности скважины она равно w = 2×p×r_c×h = 2×3,14×0,1×5 = 3,14 м². Закон Дарси выполняется, если число Рейнольдса меньше критического, которое принимаем равным Re_кр = 1. Так, как выполняется условие Re = 7,34×10^‑4 < Re_кр = 1, то закон Дарси выполняется.

Ответ: Q = 2,17 10^-4 м³/с; p(10) = 22,7 МПа; T = 4,60 года; Закон Дарси выполняется.