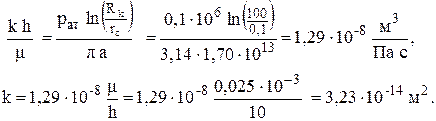Пример 3.3.

При исследовании газовой скважины на стационарном режиме получены следующие значения манометрических давлений и расходов. Построить индикаторную диаграмму. Определить коэффициент продуктивности газовой скважины, фильтрационное сопротивление и проницаемость пласта, если радиус контура питания 100 м, радиус скважины 0,1 м, толщина пласта 10 м, а вязкость газа μ = 0,025 мПа·с.

Решение:

Таблица 3.1
Qат, тыс.м3/сут	Pмс, МПа	Pс, МПа	Dp2, МПа2
0,0	49,9	50,0	0,0
86,4	49,7	49,8	15,3
172,8	49,6	49,7	34,4
259,2	49,3	49,4	57,3
345,6	49,1	49,2	84,1
432,0	48,7	48,8

 

Рис. 3.4 . Обработка результатов исследования газовой скважины на стационарных режимах при выполнении закона Дарси

Индикаторной диаграммой при фильтрации газа называется зависимость разности квадратов абсолютных давлений на контуре питания и скважине от дебита Δp² = p_k² – p_c² = f(Q_ат). Найдем абсолютные давления на скважине для первой строчки таблицы p_с = p_cm + p_ат = 49,9 + 0,1 = 50,0 МПа. Когда скважина не работает, то давление в горизонтальном пласте одинаково и равно давлению на контуре, то есть P_k = P_c0 = 50,0 МПа. Разность квадратов абсолютных давлений будет равна p_k² – p_c² = 50² – 50² = 0 МПа². Аналогично рассчитываем остальные значения и результаты заносим в таблицу. Расчетные значения в таблице выделены курсивом. По полученным данным строим индикаторную диаграмму Рис. 3.4. При фильтрации по закону Дарси, индикаторная диаграмма представляет собой прямую линию, выходящую из начала координат. При фильтрации газа закон Дарси часто нарушается при больших дебитах, поэтому отбрасываем точки, которые при больших дебитах откланяются в сторону оси Δp². По оставшимся точкам из начала координат проводим прямую линию. На этой линии выбираем точку (*) и снимаем значения координат этой точки Dp²* = 59 МПа², Q_ат* = 300 тыс.м³/сут. Находим коэффициент продуктивности скважины К и коэффициент фильтрационного сопротивления a:

По значению фильтрационного сопротивления находим коэффициент гидропроводности пласта и проницаемость пласта:

Ответ: К = 5,88∙10^-14 м³/(Па²∙с); a = 1,70∙10¹³ (Па²∙с)/м³; k = 3,23∙10^{-14 м2}.

Пример 3.4.

При исследовании газовой скважины на стационарном режиме получены следующие значения манометрических давлений и расходов. Обработать результаты исследования с учетом нарушения закона Дарси. Найти фильтрационные сопротивления “a” и “b”. Определить гидропроводность пласта. Определить дебит скважины при давлении на скважине p_мс = 39,9 МПа.

Решение:

Таблица 3.2
Q, тыс.м3/сут	Pмс, МПа	Pс, МПа	Δp2, МПа2	Δp2/Qат, МПа2 сут/тыс.м3
0,0	49,9	50,0	0,0	-
86,4	49,7	49,8	15,3	0,177
172,8	49,6	49,7	34,4	0,199
259,2	49,3	49,4	57,3	0,221
345,6	49,1	49,2	84,1	0,243
432,0	48,7	48,8	114,7	0,266

 

Рис. 3.5 . Обработка результатов исследования газовой скважины на стационарных режимах при нарушении закона Дарси.

Обработка результатов исследования газовых скважин с учетом нарушения закона Дарси проводится в координатах y = (p_k² – p_c²)/Q_ат и x = Q_ат. В этих координатах теоретическая зависимость при фильтрации по двухчленному закону фильтрации представляет собой прямую линию y = a + b x. Поэтому, как и в предыдущем примере, рассчитываем абсолютное давление p_c, разность квадратов абсолютных давлений Δp² = p_k² – p_c², но кроме того рассчитываем отношение разности квадратов давлений к дебиту скважины. При дебите Q_ат = 0 это отношение невозможно рассчитать, так, как возникает неопределенность 0/0, поэтому в последнем столбце ставим прочерк. Все результаты заносим в таблицу 3.2. По результатам расчета откладываем полученные точки на графике в координатах Δp²/Q_ат и Q_ат (Рис. 3.5). По полученным точкам проводим прямую линию. Коэффициент фильтрационного сопротивления “a” представляет собой отрезок который отсекает линия при Q_ат = 0. Из графика находим a = 0,155 МПа²∙сут/тыс.м³. Коэффициент фильтрационного сопротивления “b” представляет собой тангенс угла наклона линии к горизонту. Для его нахождения выберем точку на прямой (*) и снимем значения координат этой точки y* = 0,23 МПа²∙сут/тыс.м³, x* = 300 тыс.м³/сут. Так, как точка лежит на прямой, то она удовлетворяет этой прямой, поэтому y* = a + b x*. Откуда найдем:

В системе СИ коэффициенты “a” и ”b” будут равны:

Коэффициент “a” связан с гидропроводностью пласта соотношением

Для нахождения дебита скважины при давлении на скважине p_мс = 39,9 МПа найдем абсолютное давление p_с = 39,9 + 0,1 = 40,0 МПа и разность квадратов давлений p_k² – p_c² = 50² – 40² = 900 МПа². Тогда:

Ответ: a = 1,34∙10¹³ (Па²∙с)/м³; b = 1,87∙10¹² Па²∙с²/м⁶; Q_ат = 18,6 м³/с.

Задача 3.1

Определить значение числа Рейнольдса у стенки гидродинамически несовершенной по характеру вскрытия газовой скважины если известно, что эксплуатационная колонна перфорирована, на каждом погонном метре колонны прострелено 10 отверстий диаметром d_п = 10 мм, толщина пласта h = 15 м, проницаемость пласта k = мкм², пористость его m = 18%, коэффициент вязкости газа μ = 0,024 мПа·с, плотность газа ρ_ат = 0,720 кг/м³ и дебит скважины составляет Q_ат = 140 тыс.м³/сут.

Задача 3.2

Определить дебит газовой галереи шириной В = 100 м, если толщина пласта h = 10 м, расстояние до контура питания L = 300 м, коэффициент проницаемости пласта k = 0,12 мкм², динамический коэффициент вязкости газа μ = 0,022 мПа·с, манометрические давления на контуре питания p_мк = 8 МПа и давление в галерее p_мг = 4 МПа.

Задача 3.3

Определить нарушается ли закон Дарси в газовой галереи шириной В = 200 м, если толщина пласта h = 5 м, расстояние до контура питания L = 100 м, коэффициент проницаемости пласта k = 0,2 мкм², плотность и динамический коэффициент вязкости газа ρ_ат = 0,78 кг/м³, μ = 0,019 мПа·с, пористость пласта 15%, абсолютные давления на контуре питания и скважине p_к = 18 МПа; p_г = 4 МПа.

Задача 3.4

Определить давление на расстоянии 50 метров от газовой галереи шириной В = 200 м, если толщина пласта h = 15 м, расстояние до контура питания L = 200 м, коэффициент проницаемости пласта k = 0,15 мкм², динамический коэффициент вязкости нефти μ = 0,013 мПа·с, дебит галереи Q_ат = 200 м³/сут и абсолютное давление на галерее p_г = 8 МПа.

Задача 3.5

Определить дебит газовой скважины в случае установившейся плоскорадиальной фильтрации по закону Дарси, если известно, что манометрические давления на контуре питания и забое скважины p_мк = 18 МПа, p_мс = 10 МПа, коэффициент проницаемости пласта k = 0,3 мкм², толщина пласта h = 15 м, диаметр скважины D_с = 20 см, радиус контура питания R_k = 1 км, динамический коэффициент вязкости газа μ = 0,014 мПа·с.

Задача 3.6

Определить нарушается ли закон Дарси на расстоянии 1 м от газовой скважины, если известно, что абсолютные давления на контуре питания и забое скважины p_к = 8 МПа, p_с = 3 МПа, коэффициент проницаемости пласта k = 0,3 мкм², толщина пласта h = 10 м, диаметр скважины D_с = 20 см, радиус контура питания R_k = 100 м, плотность и динамический коэффициент вязкости газа ρ_ат = 0,77 кг/м³, μ = 0,0180 мПа·с, пористость пласта 12%.

Задача 3.7

Определить давление на расстоянии 3 м от газовой скважины в случае установившейся плоскорадиальной фильтрации по закону Дарси, если известно, что манометрическое давление на контуре питания p_мк = 27,9 МПа, коэффициент проницаемости пласта k = 0,3 мкм², толщина пласта h = 15 м, диаметр скважины D_с = 20 см, радиус контура питания R_k = 1 км, динамический коэффициент вязкости газа μ = 0,019 мПа·с. Дебит скважины Q_ат = 86,4 тыс.м³/сут.

Задача 3.8

По модели пласта в виде керна диаметром 2 см и длиной 5 см за десять минут прокачан объем газа W_ат = 2 м³. Определить коэффициент проницаемости керна, если известно, что манометрические давления на входе и на выходе в модель равны p_м1 = 1,2 МПа, p_м2 = 0,0 МПа, динамический коэффициент вязкости газа μ = 0,018 мПа·с.

Задача 3.9

Построить индикаторную диаграмму для газовой совершенной скважины, если известно, что абсолютное давление на контуре питания p_k = 8,82 МПа, коэффициент проницаемости пласта k = 0,06 мкм², толщина пласта h = 10 м, диаметр скважины D_с = 24,8 см, расстояние от оси скважины до контура питания R_k = 10 км и динамический коэффициент вязкости газа μ = 0,015 мПа∙с. Фильтрации происходит по закону Дарси.

Задача 3.10

Газовая скважина радиусом r_c = 0,1 м и контуром питания R_k = 250 м при манометрическом давлении на скважине p_мс = 8,9 МПа дают дебит 100 тыс.м³/сут. Определить дебит скважины при манометрическом давлении на скважине p_мс1 = 11,9 МПа, если давление на контуре питания p_мк = 18,9 МПа.

Задача 3.11

Определить абсолютное давление на контуре питания в случае установившейся плоскорадиальной фильтрации по закону Дарси, если известно, что манометрическое давление на забое скважины p_мс = 14,9 МПа, коэффициент проницаемости пласта k = 0,06 мкм², толщина пласта h = 15 м, диаметр скважины D_с = 20 см, радиус контура питания R_k = 500 м, динамический коэффициент вязкости газа μ = 0,019 мПа·с. Дебит скважины Q_ат = 864 тыс.м³/сут.

Задача 3.12

Определить абсолютное давление на расстояниях r₁ = 1 м и r₂ = 10 м, если происходит установившейся плоскорадиальная фильтрации по закону Дарси. Манометрические давления на контуре питания и скважине равны p_мк = 24,9 МПа, p_мс = 14,9 МПа, диаметр скважины D_с = 20 см, радиус контура питания R_k = 500 м. Построить кривую изменение давления вокруг скважины.

Задача 3.13 При исследовании газовой скважины на стационарном режиме получены следующие значения манометрических давлений и расходов. Определить гидропроводность пласта, если радиус контура питания 100 м, радиус скважины 0,1 м.
Q, м3/сут	Pмс, МПа
0,0	19,9
8,1	19,4
15,8	18,9
24,3	18,4
31,7	17,9
37,0	17,4
Задача 3.14 При исследовании газовой скважины на стационарном режиме получены следующие значения манометрических давлений и расходов. Определить проницаемость пласта, если радиус контура питания 150 м, радиус скважины 0,1 м, толщина пласта 10 м, а вязкость газа μ = 0,021 мПа·с.
Q, м3/сут	Pмс, МПа
0,0	49,9
8,6	48,8
17,2	47,9
25,9	46,8
34,5	45,9
40,2	44,8
Задача 3.15 При исследовании газовой скважины на стационарном режиме получены следующие значения манометрических давлений и расходов. Определить толщину пласта, если радиус контура питания 250 м, радиус скважины 0,1 м, проницаемость пласта k = 0,3 мкм2, а вязкость газа μ = 0,017 мПа·с.
Q, м3/сут	Pмс, МПа
0,0	24,9
10,0	24,5
20,0	24,0
30,0	23,6
40,0	23,1
50,0	21,5
Задача 3.16 При исследовании газовой скважины на стационарном режиме получены следующие значения манометрических давлений и расходов. Определить гидропроводность пласта, если радиус контура питания 200 м, радиус скважины 0,1 м.
Q, м3/сут	Pмс, МПа
0,0	24,9
24,1	23,9
47,9	22,9
72,2	21,9
95,8	20,9
110,0	19,9
Задача 3.17 При исследовании газовой скважины на стационарном режиме получены следующие значения манометрических давлений и расходов. Обработать результаты с учетом нарушения закона Дарси. Определить гидропроводность пласта, если радиус контура питания 100 м, радиус скважины 0,1 м.
Q, м3/сут	Pмс, МПа
0,0	19,9
8,1	19,4
15,8	18,9
24,3	18,4
31,7	17,9
37,0	17,4
Задача 3.18 При исследовании газовой скважины на стационарном режиме получены следующие значения манометрических давлений и расходов. Обработать результаты с учетом нарушения закона Дарси. Определить проницаемость пласта, если радиус контура питания 150 м, радиус скважины 0,1 м, толщина пласта 10 м, а вязкость газа μ = 0,025 мПа·с.
Q, м3/сут	Pмс, МПа
0,0	49,9
8,6	48,8
17,2	47,9
25,9	46,8
34,5	45,9
40,2	44,8
Задача 3.19 При исследовании газовой скважины на стационарном режиме получены следующие значения манометрических давлений и расходов. Обработать результаты с учетом нарушения закона Дарси. Определить толщину пласта, если радиус контура питания 250 м, радиус скважины 0,1 м, проницаемость пласта k = 0,3 мкм2, а вязкость нефти μ = 0,015 мПа·с.
Q, м3/сут	Pмс, МПа
0,0	24,9
10,0	24,5
20,0	24,0
30,0	23,6
40,0	23,1
50,0	21,5
Задача 3.20 При исследовании газовой скважины на стационарном режиме получены следующие значения манометрических давлений и расходов. Обработать результаты с учетом нарушения закона Дарси. Определить коэффициенты фильтрационных сопротивлений A и B.
Q, м3/сут	Pмс, МПа
0,0	24,9
24,1	23,9
47,9	22,9
72,2	21,9
95,8	20,9
110,0	19,9