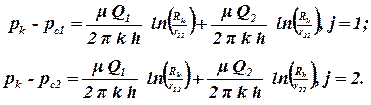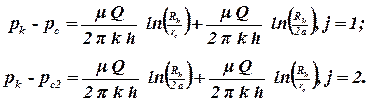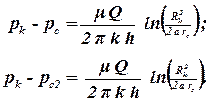Такая задача может возникнуть при расположении добывающей скважины возле сброса или около границы выклинивания продуктивного пласта. Рассмотрим скважину радиусом rc расположенную на расстоянии a от непроницаемой границе. На скважине и на контуре питания поддерживаются давления pc и pk. Необходимо найти дебит скважины Q, распределение давления и скоростей фильтрации в любой точке пласта.
Рис. 4.3. a, b  . Схемы притока к скважине у непроницаемой границе a) и в неограниченном пласте b) . Схемы притока к скважине у непроницаемой границе a) и в неограниченном пласте b)
|
Рис. 4.4  . Пример применения метода отражения для прямолинейного контура питания . Пример применения метода отражения для прямолинейного контура питания
|
Так, как граница непроницаемая, то скорость фильтрации перпендикулярно границе равна нулю, а фильтрация происходит только вдоль границы (ut ¹ 0, un = 0). Рассмотрим два случая задачи, в первом непроницаемая граница есть, а во втором случае она отсутствует (рис. 4.4). Выберем на непроницаемой границе тоску M, а во втором случае аналогичную точку в неограниченном пласте. Сравнивая оба рисунка, видим, что векторы скорости в аналогичных точках пласта направлены в разные стороны. У непроницаемой границы скорость направлена вдоль границы ut, а в неограниченном пласте к скважине u1. Для того, чтобы вектор скорости в неограниченном пласте был направлен вдоль пунктирной линии, необходимо в точке M создать вектор скорости u2. Величину и направление этого вектора найдем из условия 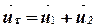 . Вектор скорости u2 в точке M можно создать, введя фиктивную добывающую скважину расположенной в точке зеркального отражения начальной скважины относительно непроницаемой границы. После такого преобразования векторы скоростей в правых частях пласта с непроницаемой границей и в неограниченном пласте будут идентичными. Отсюда следует метод отражения для непроницаемой границы. Для того, чтобы избавиться от непроницаемой границы необходимо всю область фильтрации зеркально отразить относительно этой границы. После этого непроницаемую границу можно убрать. На рис. 4.4 приведен пример использования этого метода для нескольких скважин в пласте.
. Вектор скорости u2 в точке M можно создать, введя фиктивную добывающую скважину расположенной в точке зеркального отражения начальной скважины относительно непроницаемой границы. После такого преобразования векторы скоростей в правых частях пласта с непроницаемой границей и в неограниченном пласте будут идентичными. Отсюда следует метод отражения для непроницаемой границы. Для того, чтобы избавиться от непроницаемой границы необходимо всю область фильтрации зеркально отразить относительно этой границы. После этого непроницаемую границу можно убрать. На рис. 4.4 приведен пример использования этого метода для нескольких скважин в пласте.
Для расчета дебита скважины расположенной у непроницаемой границы воспользуемся не исходной задачей, а задачей полученной с использованием метода отражения. Пронумеруем скважины: исходная скважина – 1, а фиктивная скважина – 2. Обозначим дебит исходной скважины Q1 = Q, а дебит фиктивной нагнетательной Q2 = Q. Геометрические размеры реальной и фиктивной скважины одинаковы, давление на забое первой скважины pc1 = pc. Расстояния от центра скважины до боковой поверхности этой – же скважины равны r11 = r22 = rc, а расстояние между скважинами r12 = r21 = 2a. Запишем систему уравнений интерференции для двух скважин (n = 2):
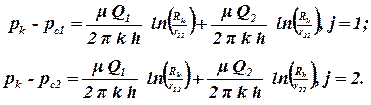
| (4.11)
|
Подставляя переменные, получим:
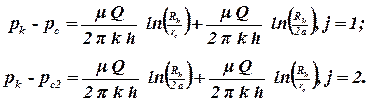
| (4.12)
|
Преобразуем полученные уравнения, используя свойства логарифмов:
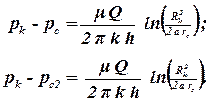
| (4.13)
|
Из первого уравнения найдем дебит скважины, расположенной у непроницаемой границы. Вычитая из первого уравнения второе найдем давление на забое фиктивной скважины:

| (4.14)
|

 . Схемы притока к скважине у непроницаемой границе a) и в неограниченном пласте b)
. Схемы притока к скважине у непроницаемой границе a) и в неограниченном пласте b)
 . Пример применения метода отражения для прямолинейного контура питания
. Пример применения метода отражения для прямолинейного контура питания
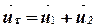 . Вектор скорости u2 в точке M можно создать, введя фиктивную добывающую скважину расположенной в точке зеркального отражения начальной скважины относительно непроницаемой границы. После такого преобразования векторы скоростей в правых частях пласта с непроницаемой границей и в неограниченном пласте будут идентичными. Отсюда следует метод отражения для непроницаемой границы. Для того, чтобы избавиться от непроницаемой границы необходимо всю область фильтрации зеркально отразить относительно этой границы. После этого непроницаемую границу можно убрать. На рис. 4.4 приведен пример использования этого метода для нескольких скважин в пласте.
. Вектор скорости u2 в точке M можно создать, введя фиктивную добывающую скважину расположенной в точке зеркального отражения начальной скважины относительно непроницаемой границы. После такого преобразования векторы скоростей в правых частях пласта с непроницаемой границей и в неограниченном пласте будут идентичными. Отсюда следует метод отражения для непроницаемой границы. Для того, чтобы избавиться от непроницаемой границы необходимо всю область фильтрации зеркально отразить относительно этой границы. После этого непроницаемую границу можно убрать. На рис. 4.4 приведен пример использования этого метода для нескольких скважин в пласте.