Рассмотрим скважину радиусом rc расположенную на расстоянии a от прямолинейного контура питания. На скважине и на контуре питания поддерживаются давления pc и pk. Необходимо найти дебит скважины Q, распределение давления и скоростей фильтрации в любой точке пласта.
Так, как давление на контуре питания постоянно, то скорость фильтрации вдоль контура питания равна нулю, а фильтрация происходит только перпендикулярно к контуру питания (ut = 0. un ¹ 0). Рассмотрим два случая задачи, в первом прямолинейный контур питания есть, а во втором случае он отсутствует (рис. 4.5 a, b). Выберем на контуре питания точку M, а во втором случае аналогичную точку в неограниченном пласте.
Рис. 4.5  . Схемы притока к скважине у прямолинейного контура питания a) и в неограниченном пласте b) . Схемы притока к скважине у прямолинейного контура питания a) и в неограниченном пласте b)
|
Рис. 4.6  . Пример применения метода отражения для прямолинейного контура питания . Пример применения метода отражения для прямолинейного контура питания
|
Сравнивая рисунки, видим, что векторы скорости в аналогичных точках пласта направлены в разные стороны. У прямолинейного контура питания перпендикулярно ему un, а в неограниченном пласте к скважине u1. Для того, чтобы вектор скорости в неограниченном пласте был направлен перпендикулярно пунктирной линии, необходимо в точке M создать вектор скорости u2. Величину и направление этого вектора найдем из условия 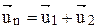 Вектор скорости u2 в точке M можно создать, введя фиктивную нагнетательную скважину расположенной в точке зеркального отражения нагнетательной скважины относительно контура питания. После такого преобразования векторы скоростей в правых частях пласта с прямолинейным контуром питания и в неограниченном пласте будут идентичными. Отсюда следует метод отражения для прямолинейного контура питания. Для того, чтобы избавиться от прямолинейного контура питания необходимо всю область фильтрации зеркально отразить относительно этого контура и в отраженной области заменить добывающие скважины – нагнетательными, а нагнетательные скважины – добывающими. После этого прямолинейный контур питания можно убрать. На рис. 4.6 приведен пример использования этого метода для нескольких скважин в пласте.
Вектор скорости u2 в точке M можно создать, введя фиктивную нагнетательную скважину расположенной в точке зеркального отражения нагнетательной скважины относительно контура питания. После такого преобразования векторы скоростей в правых частях пласта с прямолинейным контуром питания и в неограниченном пласте будут идентичными. Отсюда следует метод отражения для прямолинейного контура питания. Для того, чтобы избавиться от прямолинейного контура питания необходимо всю область фильтрации зеркально отразить относительно этого контура и в отраженной области заменить добывающие скважины – нагнетательными, а нагнетательные скважины – добывающими. После этого прямолинейный контур питания можно убрать. На рис. 4.6 приведен пример использования этого метода для нескольких скважин в пласте.
Для расчета дебита скважины у прямолинейного контура питания воспользуемся не исходной задачей, а задачей полученной с использованием метода отражения. Пронумеруем скважины: исходная скважина – 1, а фиктивная скважина – 2. Обозначим дебит исходной скважины Q1 = Q, а дебит фиктивной нагнетательной Q2 = - Q. Геометрические размеры реальной и фиктивной скважины одинаковы, давление на забое первой скважины pc1 = pc. Расстояния от центра скважины до боковой поверхности этой – же скважины равны r11 = r22 = rc, а расстояние между скважинами r12 = r21 = 2a. Запишем систему уравнений интерференции скважин с удаленным контуром питания для двух скважин (n = 2):
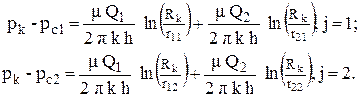
| (4.15)
|
Подставляя переменные, получим:
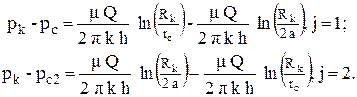
| (4.16)
|
Преобразуем полученные уравнения, используя свойства логарифмов:
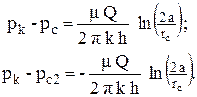
| (4.17)
|
Из первого уравнения найдем дебит скважины, расположенной у прямолинейного контура питания, а сложив эти уравнения найдем давление на забое фиктивной скважины:
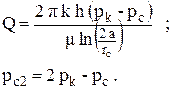
| (4.18)
|
Если бы контур питания был окружностью радиуса а = Rk, то дебит скважины рассчитывался бы по формуле Дюпюи. В реальных условиях форма контура питания часто неизвестна, но она заключена между окружностью и прямой линией. Следовательно, дебит скважины в этих условиях будет находиться в пределах
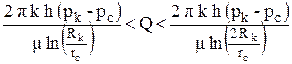 . .
| (4.19)
|

 . Схемы притока к скважине у прямолинейного контура питания a) и в неограниченном пласте b)
. Схемы притока к скважине у прямолинейного контура питания a) и в неограниченном пласте b)
 . Пример применения метода отражения для прямолинейного контура питания
. Пример применения метода отражения для прямолинейного контура питания
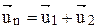 Вектор скорости u2 в точке M можно создать, введя фиктивную нагнетательную скважину расположенной в точке зеркального отражения нагнетательной скважины относительно контура питания. После такого преобразования векторы скоростей в правых частях пласта с прямолинейным контуром питания и в неограниченном пласте будут идентичными. Отсюда следует метод отражения для прямолинейного контура питания. Для того, чтобы избавиться от прямолинейного контура питания необходимо всю область фильтрации зеркально отразить относительно этого контура и в отраженной области заменить добывающие скважины – нагнетательными, а нагнетательные скважины – добывающими. После этого прямолинейный контур питания можно убрать. На рис. 4.6 приведен пример использования этого метода для нескольких скважин в пласте.
Вектор скорости u2 в точке M можно создать, введя фиктивную нагнетательную скважину расположенной в точке зеркального отражения нагнетательной скважины относительно контура питания. После такого преобразования векторы скоростей в правых частях пласта с прямолинейным контуром питания и в неограниченном пласте будут идентичными. Отсюда следует метод отражения для прямолинейного контура питания. Для того, чтобы избавиться от прямолинейного контура питания необходимо всю область фильтрации зеркально отразить относительно этого контура и в отраженной области заменить добывающие скважины – нагнетательными, а нагнетательные скважины – добывающими. После этого прямолинейный контур питания можно убрать. На рис. 4.6 приведен пример использования этого метода для нескольких скважин в пласте.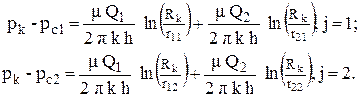
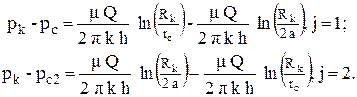
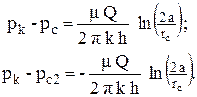
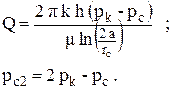
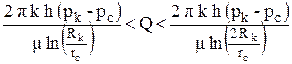 .
.



