Определение объема выборки при оценке среднего.
Рассмотрим случай, когда генеральная дисперсия известна. Дисперсия генеральной совокупности
Доверительный уровень того, что построенный интервал будет содержать в себе генеральное среднее, часто принимается 95%. При этом коэффициент Стьюдента (tc) равен примерно 2. И так как размер заданного полуинтервала (Н) определяется:
то можно относительно определить объем выборки, т.к. Н и tc заданы, а s известна из предыдущих исследований.
Например, предположим, что руководитель туристического агентства задался целью узнать средние годовые расходы рыболовов на питание и проживание во время их походов. При помощи простой случайной выборки нужно оценить среднегодовые расходы этих рыболовов, пользуясь списком лиц, получивших в течение года рыболовные лицензии. При этом заказчик хочет, чтобы оценка находилась в интервале ± $ 25 от истинного генерального значения. Таким образом, общая точность будет составлять $ 50, а половинная точность, которую будем обозначать Н, составит $ 25. Нужно определиться с доверительным уровнем результата. Пусть доверительный уровень того, что построенный интервал будет содержать в себе генеральное среднее, примем равным 95 %. При этом tx- равно примерно 2. Предположим, что определенная прежде дисперсия генеральной совокупности равна $100. Тогда Таким образом, для оценки среднего уровня расходов при среднеквадратическом отклонении $100 и заданной точности плюс или минус $25 достаточно взять сравнительно небольшую выборку (64 рыболова). Другой способ решения проблемы оценки заключается в построении номограммы уравнения и считывания с нее потребного объема выборки. Номограммы, которые, по сути, являются графическим решением уравнения, для наиболее часто используемых случаев специально разработаны и используются без предварительных расчетов. Теперь посмотрим, что произойдет, если увеличить точность исследования в 2 раза: общая ширина требуемого интервала будет равняться $25, половина его или Н, соответственно, $12,5.
Приведенное соотношение выражает зависимость точности и объема выборки. При увеличении точности в с раз, объем выборки возрастает в с2 раз. Например, если бы заданная точность оценки должна была бы вырасти в 5 раз (с=5), то объем выборки увеличился бы с 64 до 1600 (с2=25). Увеличение доверительного интервала также приводит к увеличению объема выборки, а значит к удорожанию исследований. Например, задаем не 95, а 99% доверительный интервал, тогда при Н=25, а s=100, получаем Рассмотрим случай, когда генеральная дисперсия неизвестна. Более типичным случаем является ситуация, когда генеральная дисперсия неизвестна. Однако, процедура оценки объема выборки остается практически неизменной, просто вместо известного значения дисперсии использоваться будет оценочное значение генеральной дисперсии s. Еще одна возможность заключается в учете того обстоятельства, что для величины с нормальным распределением область изменения примерно равна плюс-минус трем среднеквадратическим отклонениям. Таким образом, если можно определить область изменения, то можно путем деления на 6 определить и среднеквадратическое отклонение. Даже небольшой запас априорной информации может позволить определить область изменения. Ошибочная оценка скажется на точности доверительного интервала, которая может измениться и в большую, и в меньшую сторону. Обратимся к примеру, некоторое число рыболовов не расходует на питание и проживание никаких средств, т.к. выезжают только на день. Другие совершают несколько недельных поездок в год. Предположим, что 15 дней в году – это типичный верхний предел пребывания на рыбалке. При этом ежедневные расходы составляют около $30 долларов в неделю, т.е. верхний денежный предел равен $450. область изменения этой величины также равна $450 (т.к. потратить меньше $0 невозможно) и расчетное среднеквадратическое отклонение составляет 450/6=75. При заданной точности ± $25 и 95% доверительном интервале объем выборки составит: При проведении исследования редко анализируется только один параметр. Обычно исследования носят комплексный многоцелевой характер. Приведем пояснения в виде примера. Предположим, что необходимо определить также годовые расходы рыболовов на снасти и снаряжение и расстояние, которое они преодолевают за время рыбалок. Теперь необходимо определить уже три величины. Допустим, каждая из них тоже должна иметь 95% доверительный уровень; потребную абсолютную точность и среднеквадратическое отклонение сведем в таблицу с расчетными значениями объемов выборок, рассчитанных по формуле.
Для каждой из трех оцениваемых величин получим свое значение объема выборки. В зависимости от величины объем выборки n должен быть равным 36, 16 или 100. Необходимо определенным образом согласовать эти три значения, так чтобы принятый объем выборки отвечал сразу всем поставленным задачам. При консервативном подходе необходимо выбирать самое большое значение n=100. Этим гарантируется нужная точность оценки каждой величины при условии, что оценки среднеквадратических отклонений были корректны. Теперь рассмотрим ситуацию, когда наименее критичной их трех оцениваемых величин будет расстояние, проходимое рыболовами. Этим можно снизить расходы на исследование, используя выборку меньшего объема. Оптимальный подход в подобных ситуациях состоит в выделении наиболее критичных величин и в соответствии заданной точности и достоверности определения объема их выборки. Величины, оценка которых требует большего объема выборки, в этом случае будут оцениваться с меньшей точностью или достоверностью, чем планировалось. Предположим, что наиболее критичным показателем является уровень расходов, и остановимся на значении объема выборки 36. Предположим также, что эта выборка (состоящая из 36 рыбаков) дает выборочное среднее 300 км и выборочное отклонение
|

 s2 может быть известна из предыдущих исследований. Это означает, что размах распределения sх-, заданного среднеквадратичной ошибкой оценки известен с точностью до коэффициента пропорциональности квадратному корню из объема выборки, т.к.
s2 может быть известна из предыдущих исследований. Это означает, что размах распределения sх-, заданного среднеквадратичной ошибкой оценки известен с точностью до коэффициента пропорциональности квадратному корню из объема выборки, т.к. .
.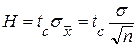 ,
,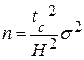 .
.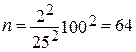 .
.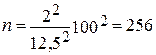 , те же данные получают и из номограммы. Т.е. для увеличения точности в 2 раза объем выборки должен быть увеличен в 4 раза.
, те же данные получают и из номограммы. Т.е. для увеличения точности в 2 раза объем выборки должен быть увеличен в 4 раза.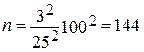 , (tc в данном случае при 99% равен 3).Таким образом, при увеличении tc в d раз (в нашем примере d=3/2), объем выборки увеличивается в d2 раз (в нашем случае d2 = 9/4). При всех вычислениях необходимо помнить о стоимости, связанной с увеличением точности и достоверности результатов.
, (tc в данном случае при 99% равен 3).Таким образом, при увеличении tc в d раз (в нашем примере d=3/2), объем выборки увеличивается в d2 раз (в нашем случае d2 = 9/4). При всех вычислениях необходимо помнить о стоимости, связанной с увеличением точности и достоверности результатов.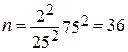 . Таким образом, отобранная выборка будет содержать 36 элементов. Предположим, что произведенные наблюдения дадут выборочное среднее
. Таким образом, отобранная выборка будет содержать 36 элементов. Предположим, что произведенные наблюдения дадут выборочное среднее  =35 и среднеквадратическое выборочное отклонение
=35 и среднеквадратическое выборочное отклонение  =60. Тогда доверительный интервал определяется:
=60. Тогда доверительный интервал определяется: 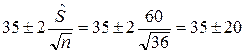 , или 15 £
, или 15 £ 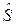 =500 км. В данном случае результат выборки согласуется с первичной оценкой генерального среднеквадратического отклонения и, соответственно, неточность никак не сказывается на доверительном интервале.
=500 км. В данном случае результат выборки согласуется с первичной оценкой генерального среднеквадратического отклонения и, соответственно, неточность никак не сказывается на доверительном интервале. или 133,3 £
или 133,3 £ 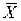 £ 466,7. В то время как заданная точность составляла ± 100 км, полученная точность равна ± 166,7 км. Для получения необходимой точности оценки доверительный уровень следует сделать меньше нынешнего 95% уровня.
£ 466,7. В то время как заданная точность составляла ± 100 км, полученная точность равна ± 166,7 км. Для получения необходимой точности оценки доверительный уровень следует сделать меньше нынешнего 95% уровня.


