Вопрос 4. Групповая (гнездовая) выборка.

Групповые выборки (кластерные) – еще один способ вероятностного выборочного исследования. Она в чем-то похожа, а в чем-то отличается от стратифицированного выборочного отбора.

Групповая выборка – вероятностная выборка, для которой характерна следующая двухступенчатая процедура: 1) генеральная совокупность делится на ряд непересекающихся исчерпывающих ее подмножеств; 2) производится случайный отбор подмножеств. Если для выборки используют все элементы выбранных подмножеств, процедура называется одноступенчатой; если же выборка отбирается из этих подмножеств при помощи вероятностного метода, процедура называется двухступенчатой.

Существуют сходства и различия групповой и стратифицированной выборки. В каждом случае генеральная совокупность делится на ряд непересекающихся, исчерпывающих ее подмножеств, однако, в стратифицированной выборке производится отбор элементов из каждого подмножества, а при групповой выборке производится отбор подмножеств.

Рассмотрим пример из вопроса 2(данные табл.1). Если все подписчики издания X будут рассматриваться в качестве первого, а все подписчики издания Y в качестве второго подмножества, можно достаточно уверено использовать в качестве контрольной выборки для оценки среднего уровня доходов ту или иную группу. Хотя распределение уровня доходов внутри каждого подмножества может отличаться от аналогичного распределения в генеральной совокупности, разброс значений уровня доходов таков, что при оценке среднего уровня доходов и дисперсии этого уровня по элементам любой из двух названных выборок можно допустить лишь незначительную ошибку.

Систематическая выборка – один из видов группового выборочного отбора, обеспечивающий возможность простейшего исследования многих генеральных совокупностей. Такая выборка предполагает включение в нее каждого k-го элемента генеральной совокупности, начиная с некоторого выбранного произвольно элемента. Рассмотрим старую совокупность из 20 индивидов и представим, что необходимо отобрать из них 5 элементов. Для 20 элементов совокупности и объема выборки, равного5, выборочная доля равна f=n/N=5/20=1/4, т.е. должен отбираться один элемент из четырех. Выборочный интервал I=1/f будет равен 4. это означает, что после произвольно выбранной начальной позиции должен отбираться каждый четвертый элемент. Если начальная позиция придется на 1, то в выборку будут отобраны 1-й, 5-й, 9-й, 13-й, 17-й элементы. Если позиция придется на 2, будут отобраны, соответственно, 2-й, 6-й, 10-й, 14-й, 18-й элементы и т.д.

Систематическая выборка относится к категории групповых одноступенчатых, т.к. используются все элементы выделенных групп, а не некоторая, возникающая в результате отбора их часть.

Подмножества или группы в нашем случае это:

Группа 1: A, E, I, M, Q.

Группа 2: B, F, J, N, R.

Группа 3: C, G, K, O, S.

Группа 4: D, H, L, P, T.

Для исследования производится случайный выбор одной из этих групп. В данном случае выбор делается один раз.

Достоинства систематической выборки:

- простота формирования;

- отсутствует проблема дублирования элементов в отличие от случайной выборки;

- имеет большую репрезентативность, чем простая случайная выборка.

При использовании систематической выборки существует следующая опасность, если в списке элементов наблюдается естественная периодичность, оценка, производимая на основе такой выборки, связана с серьезными ошибками. Например, известен уровень продаж авиабилетов на каждый день года, и нужно проанализировать продажи с точки зрения продолжительности полета. Анализ всех 365 дней года будет весьма дорогостоящим. Предположим, что исследовательского бюджета хватит на исследование 52 дней. Систематическая выборка с выборочным интервалом равным 7 дней (365/52) скорее всего, приведет к ошибочным выводам, т.к. будет отражать уровень продаж авиабилетов на рейсы, совершаемые по понедельникам, средам или, например, по воскресеньям.

Поэтому, правильное задание выборочного интервала возможно только на основе исследования причин периодичности.

Территориальная выборка – вид группового выборочного отбора, при котором территории или зоны (например, переписные районы, участки) выступают в роли первичных выборочных единиц. Генеральная совокупность делится (обычно с использованием карты) на ряд непересекающихся, исчерпывающих ее подмножеств или территорий, после чего формируется случайная выборка этих территорий. Если в исследовании участвуют все семьи, живущие на выделенных территориях, то имеем дело с одноступенчатой территориальной выборкой; если же исследуются не все, но лишь отобранные из первичной выборки семьи, обследование называется двухступенчатым.

Принцип, который лежит в основе систематической выборки, задействован и в территориальном выборочном отборе.

Составить точные исчерпывающие списки населения практически невозможно. Либо они просто отсутствуют, либо если и существуют, то содержат массу устаревшей недостоверной информации (люди переезжают, рождаются, умирают, женятся и разводятся). Несмотря на отсутствие списка семей, можно использовать в качестве относительно точных первичных выборочных единиц отдельные городские районы, представленные на карте.

Одноступенчатая территориальная выборка проводится на основе следующих этапов:

1) Произвести простой случайный отбор n городских кварталов из совокупности N кварталов.

2) Определить потребление товара и доходы всех семей, живущих в выделенных кварталах, и распространить выборочный показатель на всю совокупность.

Отличительной особенностью одноступенчатой территориальной выборки является регистрация и исследование всех семей, проживающих в выделенных территориальных единицах. Часто вместо сплошного исследования всех элементов выделенной группы проводится только выборочное обследование. Различают два типа двухступенчатой территориальной выборки.

1). Простая двухступенчатая территориальная выборка.

2). Территориальная выборка с вероятностями, пропорциональными объему (территориальная квотная выборка).

Простая двухступенчатая территориальная выборка – вид группового выборочного отбора, при котором из каждой первичной выборочной единицы (например, районов) отбирается определенная доля элементов выборки второго уровня (например, семей).

Рассмотрим совокупность, состоящую из 100 кварталов предположим, что в каждом квартале живут по 20 семей. Допустим, необходимо исследовать 80 семей из 2000. Таким образом, выборочная доля равна

.

Существует ряд способов формирования выборки:

1). Отбор 10 кварталов и 8 семей в каждом квартале;

2). Отбор 8 кварталов и 10 семей в каждом квартале;

3). Отбор 20 кварталов и 4 семей в каждом квартале;

4). Отбор 4 кварталов и 20 семей в каждом квартале.

Последний вариант представляет собой одноступенчатую территориальную выборку, а первые три относятся к категории двухступенчатых. Варианты, с которой будут отобраны кварталы, называются первоуровневой выборочной долей.

,

где n_k и N_k – количество кварталов в генеральной совокупности и в выборке соответственно. Для первых трех случаев первоуровневые выборочные доли равны, соответственно 1/10, 1/12,5 и 1/5.

Вероятность отбора семьи называется выборочной долей второго уровня. Т.к. выборка должна состоять из 80 семей, выборочная доля второго уровня отличается для каждого из приведенных выше вариантов.

_,

где n_k/c и N_k/c – количество семей на квартал в выборке и в генеральной совокупности. Для первых трех схем отбора выборочная доля равна соответственно: 8/20=2/5, 10/20=1/2, 4/20=1/5. При этом, произведение выборочных долей первого и второго уровней в любом случае равно общей выборочной доле 1/25. из соображения экономии при сборе данных выборочная доля второго уровня должна быть высокой (вторая схема), но из соображений статистической эффективности выборочная доля второго уровня должна быть небольшой. Поэтому статистические соображения свидетельствуют в пользу третьей схемы. Простая двухступенчатая территориальная выборка эффективна, если количество единиц второго уровня (семья) на единицу первого уровня (квартал) сохраняется примерно равным. Если количество единиц второго уровня существенно отличаются друг от друга, простая двухступенчатая выборка может привести к ошибочным оценкам. Например, в некоторых кварталах могут находиться многоэтажные дома, где проживают семьи с низким доходом. В богатых кварталах могут находиться всего несколько домов, в каждом из которых будет проживать по одной семье. Т. е., количество единиц второго уровня на единицу первого уровня окажется совершенно различным. Проблема эта снимается путем комбинирования различных территорий, или прибегают к территориальной квотной выборке.

Территориальная квотная выборка – вид группового отбора, при котором из каждой первичной выборочной единицы отбирается фиксированное количество элементов второго уровня. Вероятности, относящиеся к отбору каждой первичной единицы, могут изменяться, т.к. они напрямую связаны с относительными размерами первичных единиц.

Приведем пример на основании предыдущего.

Квартал	Количество семей	Суммарное количество семей
1 2 3 4 5 6 7 8 9 10	800 400 200 200 100 100 100 50 25 25	800 1200 1400 1600 1700 1800 1900 1950 1975 2000

Пусть после анализа экономических и статистических критериев количество единиц второго уровня на единицу первого уровня было принято равным 10.для получения выборки нужного объема (20 единицам) необходимо выбрать две единицы первого уровня. Вероятность выбора определенного элемента зависит от объема единицы первого уровня. В данном случае можно прибегнуть к таблицам трехзначных случайных чисел. Для этого можно воспользоваться двумя первыми числами от 1 до 2000. Числа от 1 до 800 относятся к первому кварталу; числа от 801 до 1200 – ко второму кварталу; числа от 1201 до 1400 – к третьему и т.д.

Вероятность того, что в выборку будет включена любая конкретная семья, остается постоянной, т.к. отличия вероятностей отбора элементов первого уровня компенсируются отличиями вероятностей отбора элементов второго уровня. Допустим, к примеру, рассмотрим два полюса – 1-й и 10-й кварталы. Вероятность выделения квартала 1 равна 800/2000=2/5, т.к. 800 из возможных 2000 значений случайных чисел приходится именно на этот квартал. Кварталу 10 соответствует только 25 значений случайных чисел (от 1976 до 2000), соответственно выборочная доля первого уровня для 10 квартала равна 25/2000=1/80. Т. к. из каждого квартала следует выбрать по 10 семей, выборочная доля второго уровня для первого квартала равна 10/800=1/80, для 10 квартала 10/25=1/2,5. При перемножении соответствующих вероятностей первого и второго уровней происходит их компенсация

.

Подобное соотношение верно и для других кварталов.

Достоинства территориальной квотной выборки:

- возможность избежать ошибок, присущих простой двухступенчатой территориальной выборке;

- повышение точности оценок при увеличении изменчивости количества единиц второго уровня на единицу первого уровня.

-
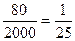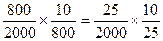