Несжимаемая жидкость в недеформируемом пластеВыразим скорость фильтрации через дебит Q u=Q / (2p rh) и перепишем выражение (3.46) в виде
Отсюда, разделяя переменные и интегрируя, в первом случае, по радиусу от r до Rк и по давлению от р до рк, а, во втором случае, по радиусу от rс до Rк и по давлению от рс до рк, получим: распределение давления в пласте
дебит скважины
Дебит находится как положительный корень квадратного уравнения (3.48). Из данного уравнения видно, что индикаторная линия - парабола. Кривая распределения давления (3.47) - гипербола и воронка депрессии - гипербола вращения. Крутизна воронки депрессии у стенки скважины будет больше, чем у чисто логарифмической кривой при течении по закону Дарси.
|
.
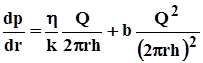; 3.47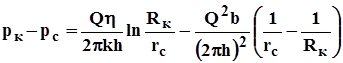
. 3.48
