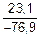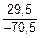Пример Г.12
Построить эпюры реактивных давлений грунта, поперечных сил и изгибающих моментов для балки на упругом основании, показанной на рисунке Г.7.
Дано: Длина балки L = 8 м, ширина b = 1 м, жесткость балки равна 256,8 МПа·м4, модуль общей деформации основания Е о = 42 МПа, коэффициент поперечных деформаций n = 0,35.
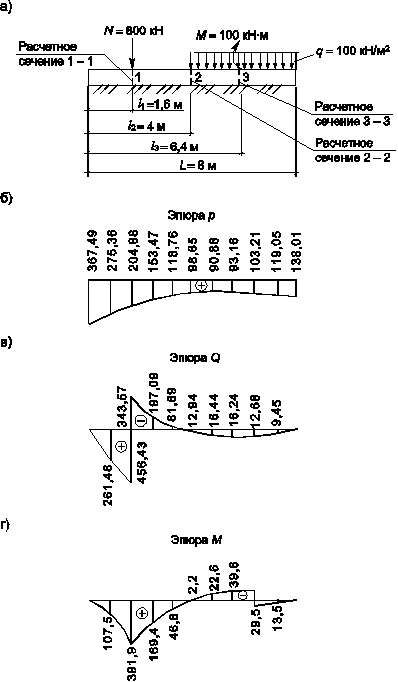
Рисунок Г.7 — Расчетная схема балки и эпюры р, Q, М к примеру Г.12:
а) расчетная схема балки;
б) эпюра реакций грунта (p);
в) эпюра поперечных сил (Q);
г) эпюра изгибающих моментов (М)
Решение. По формуле (5.72) находим показатель гибкости балки a и соотношение b = li / L для сечений 1 – 1, 2 – 2 и 3 – 3:
a = 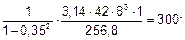
b1= 1,6/8 = 0,2;
b2 = 4/8 = 0,5;
b3 = 6,4/8 = 0,8.
Затем с помощью таблиц, приведенных в [2], находятся ординаты эпюры реактивных давлений грунта под балкой р 1 – р 3 раздельно (таблица Г.7): от силы N при показателе гибкости a = 300 и соотношении b1 = 0,2, от действия равномерно распределенной нагрузки q при показателе гибкости a = 300 и соотношении b2 = 0,5 и от действия изгибающего момента М при показателе гибкости a = 300 и соотношении b3 = 0,8 (значения р 1 – р 3 — см. таблицу Г.7). В таблицах [2] даны значения единичных ординат р для показателя b = 0,2. Из условий симметрии следует, что этому показателю соответствует также значение b = 0,8. Поэтому реактивное давление р в данном случае определяется при b = 0,2, но в обратном порядке.
Таблица Г.7 — Результаты вычислений реактивного давления грунта
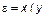
| 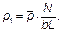 кН/м2 кН/м2
| 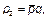 кН/м2 кН/м2
| 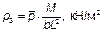
| 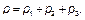 кН/м2 кН/м2
| |
| 377,7
| –5,1
| –5,11
| 367,49
| | 0,1
| 278,0
| 0,5
| –2,94
| 275,56
| | 0,2
| 200,4
| 7,2
| –2,72
| 204,88
| | 0,3
| 141,6
| 15,5
| –3,63
| 153,47
| | 0,4
| 97,9
| 25,7
| –4,84
| 118,76
| | 0,5
| 65,9
| 38,3
| –5,55
| 98,63
| | 0,6
| 42,1
| 53,7
| –4,92
| 90,88
| | 0,7
| 23,0
| 72,3
| –2,14
| 93,16
| | 0,8
| 5,0
| 94,6
| 3,61
| 103,21
| | 0,9
| –15,2
| 121,1
| 13,15
| 119,40
| | 1,0
| –41,2
| 151,9
| 27,31
| 138,01
|
Реактивное давление грунта р от совместного действия усилий N, q и М определяется исходя
из принципа независимости действия сил посредством простого сложения значений соответствующих ординат. Результаты вычислений суммарных значений ординат реактивного давления грунта р приведены в последнем столбце таблицы Г.7 и на рисунке Г.7б).
Аналогичным образом в таблицах, приведенных в [2], находятся ординаты эпюр поперечных сил Q 1 и Q 2 и изгибающих моментов М 1 и М 2 раздельно: от действия на балку только сосредоточенной силы N при a = 300 и b1 = 0,2 и от действия равномерно распределенной нагрузки q при a = 300
и b2 = 0,5.
Для показателей гибкости подсчет ординат эпюры поперечных сил Q 3 от действия на балку изгибающего момента М при a = 300 и b3 = 0,8 производится при b = 0,8, что из условий симметрии соответствует b = 0,2, но в обратном порядке. Результаты вычислений поперечных сил сведены в таблицу Г.8 и представлены на рисунке Г.7в).
| Таблица Г.8 — Результаты вычислений поперечных сил
|
| 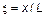
| 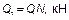
| 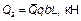
| 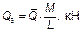
| 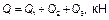
| | |
|
|
|
|
| | | 0,1
| 260,8
| –2,4
| 3,08
| 261,48
| | | 0,2
| 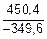
| 0,8
| 5,23
| 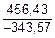
| | | 0,3
| –214,4
| 9,6
| 7,71
| –197,09
| | 0,4
| –119,2
| 26,4
| 11,11
| –81,69
| | 0,5
| –54,4
| 52,0
| 15,34
| 12,94
| | 0,6
| –12,0
| 8,8
| 19,64
| 16,44
| | 0,7
| 14,4
| –20,8
| 22,64
| 16,24
| | 0,8
| 24,0
| –34,4
| 22,28
| 12,68
| | 0,9
| 29,4
| –28,8
| 15,85
| 9,45
| | 1,0
|
|
|
|
| | Примечание — Над чертой приведены значения ординат — слева, под чертой — справа от сечения.
| | | | | | | | | |
Для показателей гибкости a = 300 и b2 = 0,5 подсчет ординат изгибающих моментов М 3 от действия силы N для a = 300 и b3 = 0,8 производится из условия симметрии при b = 0,1.
Суммарный изгибающий момент М, возникающий в поперечных сечениях балки от совместного действия сосредоточенной силы, равномерно распределенной нагрузки и изгибающего момента, определяется согласно принципу независимости действия сил сложением соответствующих значений ординат изгибающих моментов (таблица Г.9). Эпюра изгибающих моментов представлена на рисунке Г.7г).
Таблица Г.9 — Результаты вычислений изгибающих моментов
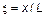
| 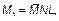 кН∙м кН∙м
| 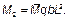 кН∙м кН∙м
| 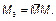 кН∙м кН∙м
| 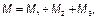 кН∙м кН∙м
| |
|
|
|
|
| | 0,1
| 108,8
|
| –1,3
| 107,5
| | 0,2
| 396,8
|
| –4,9
| 391,9
| | 0,3
| 179,2
|
| –9,8
| 169,4
| | 0,4
| 44,8
| 19,2
| –17,2
| 46,8
| | 0,5
| –19,2
| 44,8
| –27,8
| –2,2
| | 0,6
| –44,8
| 64,0
| –41,8
| –22,6
| | 0,7
| –44,8
| 64,0
| –58,8
| –39,6
| | 0,8
| –32
| 38,4
| 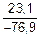
| 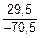
| | 0,9
| –6,4
| 12,8
| 7,1
| 13,5
| | 1,0
|
|
|
|
| | Примечание — Над чертой приведены значения ординат — слева, под чертой — справа от сечения.
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
Этические проблемы проведения экспериментов на человеке и животных В настоящее время четко определены новые подходы и требования к биомедицинским исследованиям...
Классификация потерь населения в очагах поражения в военное время Ядерное, химическое и бактериологическое (биологическое) оружие является оружием массового поражения...
Факторы, влияющие на степень электролитической диссоциации Степень диссоциации зависит от природы электролита и растворителя, концентрации раствора, температуры, присутствия одноименного иона и других факторов...
|
Механизм действия гормонов а) Цитозольный механизм действия гормонов. По цитозольному механизму действуют гормоны 1 группы...
Алгоритм выполнения манипуляции Приемы наружного акушерского исследования. Приемы Леопольда – Левицкого. Цель...
ИГРЫ НА ТАКТИЛЬНОЕ ВЗАИМОДЕЙСТВИЕ Методические рекомендации по проведению игр на тактильное взаимодействие...
|
|


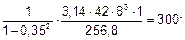
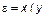
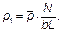 кН/м2
кН/м2
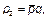 кН/м2
кН/м2
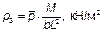
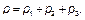 кН/м2
кН/м2
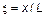
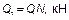
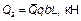
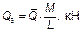
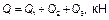
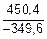
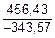
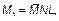 кН∙м
кН∙м
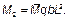 кН∙м
кН∙м
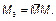 кН∙м
кН∙м
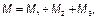 кН∙м
кН∙м