Тема: Индексы
Индексный анализ применяется для изучения явления во времени, по территориям, а также для определения влияния факторов на изменение обобщающего показателя. Индексы позволяют решить следующие задачи: 1. Определить изменение простого явления во времени. Для этого используются индивидуальные индексы, которые равны соотношению уровня явления в отчетном и базисном периодах:
2. Определить изменение сложного явления во времени. С этой целью применяют сводные (агрегатные) индексы. В зависимости от базы, на которой фиксируются соизмерители, различают индексы Пааше, Ласпейреса, Фишера, Лоу. a) Индекс Пааше (соизмеритель на отчетном уровне):
где
б) Индекс Ласпейреса (соизмеритель на базисном уровне):
где в) Индекс Лоу (соизмеритель - средняя из уровней отчетного и базисного периодов):
где г) Индекс Фишера (равен средней из индексов Пааше и Ласпейреса)
3. Определить влияние факторов на динамику сложных явлений. Для этого используется система взаимосвязанных индексов.
где
Качественным считается показатель, отражающий размер явления у 1 единицы совокупности, например, выработка 1 работника, затраты на единицу изделия, стоимость единицы товара и т.д. 4. Определить изменение среднего значения признака и рассчитать влияние факторов на его изменение. С этой целью используют систему индексов постоянного, переменного состава и индекс структурных сдвигов. а) Индекс переменного состава показывает общее изменение среднего значения признака:
б) Индекс постоянного состава позволяет определить влияние изменения осредняемого признака на общее изменение средней:
в) Индекс структурных сдвигов отражает изменение средней под воздействием изменения структуры совокупности:
Iпер. состава = Iпост. сост. · Iструкт. сдвигов, (5.14)
где
5. Определить абсолютное изменение показателей, общее и за счет отдельных факторов. Для этого из числителя соответствующего индекса вычитают знаменатель этого индекса. При этом общее абсолютное изменение показателя будет равно сумме отклонений за счет каждого из факторов. Для определения среднего индекса из индивидуальных используют средний арифметический и средний гармонический индексы. Средний арифметический индекс применяется в том случае, если известен уровень обобщающего явления в базисном периоде (
так как из формулы (5.1) Средний гармонический индекс используется тогда, когда известен уровень обобщающего явления в отчетном периоде (
так как из формулы (5.1)
где
|

 . (5.1)
. (5.1) , (5.2)
, (5.2) - уровень индексируемой величины в отчетном и базисном периодах;
- уровень индексируемой величины в отчетном и базисном периодах; - уровень соизмерителя в отчетном периоде.
- уровень соизмерителя в отчетном периоде.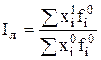 ,(5.3)
,(5.3)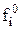 - уровень соизмерителя в базисном периоде.
- уровень соизмерителя в базисном периоде.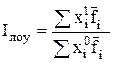 , (5.4)
, (5.4)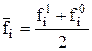 . (5.5)
. (5.5) (5.6)
(5.6)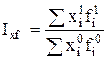
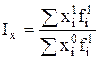

 ,
,
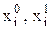 - значения качественного показателя в базисном и отчетном периодах;
- значения качественного показателя в базисном и отчетном периодах;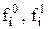 - значения количественного показателя в базисном и отчетном периодах.
- значения количественного показателя в базисном и отчетном периодах.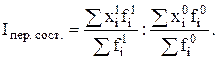 (5.11)
(5.11)
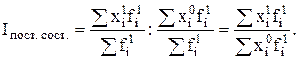 (5.12)
(5.12) (5.13)
(5.13) - значения осредняемого признака в базисном периоде;
- значения осредняемого признака в базисном периоде; - значения осредняемого признака в отчетном периоде;
- значения осредняемого признака в отчетном периоде; - вес осредняемого признака в отчетном и базисном периодах.
- вес осредняемого признака в отчетном и базисном периодах. ) и индивидуальный индекс ix. Он выводится из формулы индекса Ласпейреса (5.3).
) и индивидуальный индекс ix. Он выводится из формулы индекса Ласпейреса (5.3). , (5.15)
, (5.15) . (5.16)
. (5.16)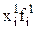 ) и получается путем преобразования в средний агрегатного индекса Пааше.
) и получается путем преобразования в средний агрегатного индекса Пааше. , (5.17)
, (5.17)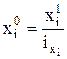 , (5.18)
, (5.18) - индивидуальные индексы;
- индивидуальные индексы; - значения обобщающего показателя в базисном и отчетном периодах.
- значения обобщающего показателя в базисном и отчетном периодах.


