Геометрическая вероятность. Одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным количеством исходов
Одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным количеством исходов. В таких случаях можно воспользоваться понятием геометрической вероятности. Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезок L и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вероятность попадания точки на любую часть отрезка L не зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вероятность того, что брошен-ная точка попадет на отрезок l, являющийся частью отрезка L, вычисляется по формуле:
где l – длина отрезка l, а L – длина отрезка L. Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вероятности того, что она попадет на часть этой области s:
где s – площадь части области, а S – площадь всей области. В трехмерном случае вероятность того, что точка, случайным образом расположенная в теле V, попадет в его часть v, задается формулой:
где v – объем части тела, а V – объем всего тела.
3.Теоремы теории вероятностей. Теорема сложения вероятностей несовместимых событий. Полная группа событий. Противоположные события. Теорема1. (теорема сложения). Вероятность р (А + В) суммы событий А и В равна Р (А + В) = р (А) + р (В) – р (АВ). (2.2) Доказательство. Докажем теорему сложения для схемы случаев. Пусть п – число возможных исходов опыта, тА – число исходов, благоприятных событию А, тВ – число исходов, благопри-ятных событию В, а тАВ – число исходов опыта, при которых происходят оба события (то есть исходов, благоприятных произведению АВ). Тогда число исходов, при которых имеет место событие А + В, равно тА + тВ – тАВ (так как в сумме (тА + тВ) тАВ учтено дважды: как исходы, благоприятные А, и исходы, благоприятные В). Следовательно, вероятность суммы можно определить по формуле (1.1):
что и требовалось доказать. Теорему1 можно распространить на случай суммы любого числа событий. Например, для суммы трех событий А, В и С Р (А + В + С) = р (А) + р (В) + р (С) – р (АВ) – р (АС) – р (ВС) + р (АВС)
Теорема 2. Сумма вероятностей противоположных событий равна 1: р (А) + р ( Так как А и Р (А + Замечание. В ряде задач проще искать не вероятность заданного события, а вероятность события, противоположного ему, а затем найти требуемую вероятность по формуле (2.5).
|

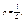 (2.1)
(2.1)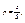 (2.1`)
(2.1`)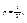 (2.1``)
(2.1``)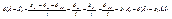
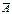 ) = 1. Доказательство.
) = 1. Доказательство.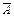 ). Значит, р (А) + р (
). Значит, р (А) + р (


