Вероятность появления хотя бы одного события.
Теорема. Вероятность появления хотя бы одного из попарно независимых событий А 1, А 2,…, Ап равна р (А) = 1 – q 1 q 2… qn, (2.9) где qi – вероятность события Доказательство. Если событие А заключается в появлении хотя бы одного события из А 1, А 2,…, Ап, то события А и
|
, противоположного событию Аi.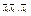
противоположны, поэтому по теореме 2.2 сумма их вероятностей равна 1. Кроме того, поскольку А 1, А 2,…, Ап независимы, то независимы и 
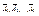, следовательно, р (
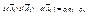. Отсюда следует справедливость формулы (2.9).
