Непрерывной называют случайную величину, которая может принимать любые значения из некоторого заданного интервала, например, время ожидания транспорта, температура воздуха в каком-либо месяце, отклонение фактического размера детали от номинального, и т.д. Интервал, на котором она задана, может быть бесконечным в одну или обе стороны. Функция распределения обладает следующими свойствами: F1) Функция распределения 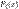 не убывает:
не убывает: 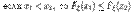 ; F2) Существуют пределы
; F2) Существуют пределы 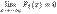 и
и  . F3) Функция распределения
. F3) Функция распределения 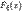 непрерывна слева:
непрерывна слева:  .
.
18. Функция распределения случайной величины, ее свойства (свойства 4-6). F4) В любой точке 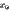 разница
разница  равна
равна  :
:  или, иначе,
или, иначе, 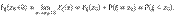
F5) Для любой случайной величины  имеет место равенство
имеет место равенство  . Если же функция распределения
. Если же функция распределения  непрерывна (для любого х, или только в точках а и b), то
непрерывна (для любого х, или только в точках а и b), то 
F6) Случайная величина 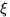 имеет дискретное распределение тогда и только тогда, когда функция распределения
имеет дискретное распределение тогда и только тогда, когда функция распределения  — ступенчатая функция. При этом возможные значения
— ступенчатая функция. При этом возможные значения  — точки ai скачков
— точки ai скачков  , и
, и  — величины скачков.
— величины скачков.

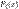 не убывает:
не убывает: 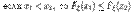 ; F2) Существуют пределы
; F2) Существуют пределы 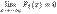 и
и  . F3) Функция распределения
. F3) Функция распределения 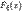 непрерывна слева:
непрерывна слева:  .
.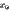 разница
разница  равна
равна  :
:  или, иначе,
или, иначе, 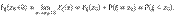
 имеет место равенство
имеет место равенство  . Если же функция распределения
. Если же функция распределения  непрерывна (для любого х, или только в точках а и b), то
непрерывна (для любого х, или только в точках а и b), то 
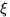 имеет дискретное распределение тогда и только тогда, когда функция распределения
имеет дискретное распределение тогда и только тогда, когда функция распределения  — ступенчатая функция. При этом возможные значения
— ступенчатая функция. При этом возможные значения  , и
, и  — величины скачков.
— величины скачков.


