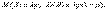Непрерывные случайные величины. Дифференциальная функция распределения (плотность вероятности).
Непрерывной называют случайную величину, которая может принимать любые значения из некоторого заданного интервала, например, время ожидания транспорта, температура воздуха в каком-либо месяце, отклонение фактического размера детали от номинального, и т.д. Интервал, на котором она задана, может быть бесконечным в одну или обе стороны. ПЛОТНОСТЬ ВЕРОЯТНОСТИ (плотность распределения вероятностей) случайной величины X - ф-ция р (х)такая, что 20. Математическое ожидание, дисперсия, среднее квадратическое отклонение непрерывной случайной величины. Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D (X) = M (X - M (X))2. Для вычислений удобнее пользоваться формулой: D (X) = M (X 2) - (M (X)) 2. Среднеквадратическим отклонением случайной величины x называется корень квадратный из дисперсии этой величины: 21. Некоторые законы распределения случайных величин: биномиальное распределение. Случайная величина В = X1 + X1 +…+ Xk называется биномиальной. Ясно, что 0<B<k при всех возможных исходах опытов. Чтобы найти распределение В, т.е. вероятности Р(В = а) при а = 0, 1, …, k, достаточно знать р – вероятность наступления рассматриваемого события в каждом из опытов. Действительно, случайное событие В = а осуществляется тогда и только тогда, когда событие А наступает ровно при а испытаниях. Если известны номера всех этих испытаний (т.е. номера в последовательности испытаний), то вероятность одновременного осуществления в а опытах события А и в k-а опытах противоположного ему – это вероятность произведения k независимых событий. Вероятность произведения равна произведению вероятностей, т.е. рa(1 - р)k-a. Сколькими способами можно задать номера а испытаний из k? Это
|

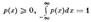 и при любых а < b вероятность события а < X < b равна
и при любых а < b вероятность события а < X < b равна 
 Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X) = x1 p1+ x2 p2+...+ xn pn. Реально на основе данных выборки мы не можем вычислить M(X). Однако эту характеристику можно оценить. В качестве оценки можно использовать среднее арифметическое, то есть M(X) ≈`X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X) = x1 p1+ x2 p2+...+ xn pn. Реально на основе данных выборки мы не можем вычислить M(X). Однако эту характеристику можно оценить. В качестве оценки можно использовать среднее арифметическое, то есть M(X) ≈`X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка.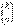 - число сочетаний из k элементов по а, рассматриваемое в комбинаторике. Как известно,
- число сочетаний из k элементов по а, рассматриваемое в комбинаторике. Как известно,  где символом k! обозначено произведение всех натуральных чисел от 1 до k, т.е.
где символом k! обозначено произведение всех натуральных чисел от 1 до k, т.е.  (дополнительно принимают, что 0! = 1). Из сказанного следует, что биномиальное распределение, т.е. распределение биномиальной случайной величины, имеет вид
(дополнительно принимают, что 0! = 1). Из сказанного следует, что биномиальное распределение, т.е. распределение биномиальной случайной величины, имеет вид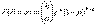 математическое ожидание и дисперсия выраж. Формулами:
математическое ожидание и дисперсия выраж. Формулами: