Закон нормального распределения случайной величины.
Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это – наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Нормальный закон распределения характеризуется плотностью вероятности вида: Нормальный закон распределения также называется законом Гаусса. 25. Закон нормального распределения: вероятность отклонения случайной величины от ее мат.ожидания, центральная предельная теорема. Центральная предельная теорема (для разнораспределенных слагаемых). Пусть X1, X2,…, Xn,… - независимые случайные величины с математическими ожиданиями М(X1), М(X2),…, М(Xn), … и дисперсиями D(X1), D(X2),…, D(Xn), … соответственно. Пусть
|
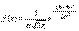
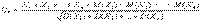Тогда при справедливости некоторых условий, обеспечивающих малость вклада любого из слагаемых в Un2, 
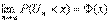для любого х.
