Теорема сложения вероятностей совместимых событий.
Теорема сложения вероятностей совместных событий:
9. Формула полной вероятности. Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2,..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A,..., HnA. Следовательно, 10. Формула Байеса. Пусть событие В происходит одновременно с одним из n несовместных событий. A1,A2…,An,Требуется найти вероятность события,Ai если известно, что событие B произошло. На основании теоремы о вероятности произведения двух событий можно написать или 11. Независимые испытания. Формула Бернулли. Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности), равна: Вероятность того, что в n испытаниях событие наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз, — находят соответственно по формулам: Pn(0)+Pn(1)+...+Р n(k-1); Pn(k+1)+Pn(k+2)+...+Pn(n); Pn(k)+Pn(k+1)+...+Pn(n); Pn(0)+Pn(1)+...+Pn(k);
|

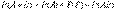 Теорема может быть обобщена на любое конечное число совместных событий
Теорема может быть обобщена на любое конечное число совместных событий При вычислении вероятности суммы большого числа событий А=А1+А2+А3+…+Аn часто бывает проще перейти к вычислению вероятности противоположного события. Для независимых событий получим формулу:
При вычислении вероятности суммы большого числа событий А=А1+А2+А3+…+Аn часто бывает проще перейти к вычислению вероятности противоположного события. Для независимых событий получим формулу: 
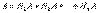 Применяя аксиому сложения вероятностей, имеем
Применяя аксиому сложения вероятностей, имеем 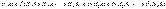 Эта формула называется формулой полной вероятности. События H1, H2,..., Hn часто называют «гипотезами».
Эта формула называется формулой полной вероятности. События H1, H2,..., Hn часто называют «гипотезами». Откуда
Откуда 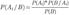
 (формула)
(формула)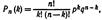 где q=1-p
где q=1-p


