Условной вероятностью Р(В / А) называется вероятность события В, вычисленная в предположении, что событие А уже наступило.
Теорема. Вероятность совместного появления двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р(А ∙ В) = Р(А)∙Р(В / А). (2.2)
Два события называются независимыми, если появление любого из них не изменяет вероятность появления другого, т.е.
Р(А) = Р(А/В или ) Р(В) = Р(В / А). (2.3)
Если события А и В независимы, то из формул (2.2) и (2.3) следует
Р(А ∙ В) = Р(А)∙ Р(В). (2.4)
Справедливо и обратное утверждение, т.е. если для двух событий выполняется равенство (2.4), то эти события независимы. В самом деле, из формул (2.4) и (2.2) вытекает
Р(А ∙ В) = Р(А)∙ Р(В) = Р(А) × Р(В / А откуда ), Р(А) = Р(В / А).
Формула (2.2) допускает обобщение на случай конечного числа событий А 1, А 2,…, А n:
Р(А 1∙ А 2∙…∙ А n)= Р(А 1)∙ Р(А 2/ А 1)∙ Р(А 3/ А 1 А 2)∙…∙ Р(А n / А 1 А 2… А n -1).
Задача 1.11. Из урны, в которой 5 белых и 10 черных шаров, вынимают подряд два шара. Найти вероятность того, что оба шара белые (событие А).
Решение. Рассмотрим события: В – первый вынутый шар белый; С – второй вынутый шар белый. Тогда А = ВС.
Опыт можно провести двумя способами:
1) с возвращением: вынутый шар после фиксации цвета возвращается в урну. В этом случае события В и С независимы:
Р(А) = Р(В)∙ Р(С) = 5/15 ×5/15 = 1/9;
2) без возвращения: вынутый шар откладывается в сторону. В этом случае события В и С зависимы:
Р(А) = Р(В)∙ Р(С / В).
Для события В условия прежние, 
, а для С ситуация изменилась. Произошло В, следовательно в урне осталось 14 шаров, среди которых 4 белых 
.
Итак,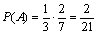 
.
Задача 1.12. Среди 50 электрических лампочек 3 нестандартные. Найти вероятность того, что две взятые одновременно лампочки нестандартные.
Решение. Рассмотрим события: А – первая лампочка нестандартная, В – вторая лампочка нестандартная, С – обе лампочки нестандартные. Ясно, что С = А ∙ В. Событию А благоприятствуют 3 случая из 50 возможных, т.е. Р(А) = 3/50. Если событие А уже наступило, то событию В благоприятствуют два случая из 49 возможных, т.е. Р(В / А) = 2/49. Следовательно,
.
Задача 1.13. Два спортсмена независимо друг от друга стреляют по одной мишени. Вероятность попадания в мишень первого спортсмена равна 0,7, а второго – 0,8. Какова вероятность того, что мишень будет поражена?
Решение. Мишень будет поражена, если в нее попадет либо первый стрелок, либо второй, либо оба вместе, т.е. произойдет событие А+В, где событие А заключается в попадании в мишень первым спортсменом, а событие В – вторым. Тогда
Р(А + В)= Р(А)+ Р(В)– Р(А ∙ В)=0, 7+0, 8–0, 7∙0,8=0,94.
Задача 1.14. В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что два учебника окажутся в переплете.
Решение. Введем обозначения событий: A – первый взятый учебник имеет переплет, В – второй учебник имеет переплет. Вероятность того, что первый учебник имеет переплет,
P(A) = 3/6 = 1/2.
Вероятность того, что второй учебник имеет переплет, при условии, что первый взятый учебник был в переплете, т.е. условная вероятность события В, такова: P(B / А) = 2/5.
Искомая вероятность того, что оба учебника имеют переплет, по теореме умножения вероятностей событий равна
P(AB) = P(A) ∙ P(B / А) = 1/2·∙ 2/5 = 0,2.
Задача 1.15. В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
Решение. Введем обозначения событий: A – первым отобран мужчина, В – вторым отобран мужчина, С – третьим отобран мужчина. Вероятность того, что первым будет отобран мужчина, P(A) = 7/10.
Вероятность того, что вторым отобран мужчина, при условии, что первым уже был отобран мужчина, т.е. условная вероятность события В следующая: P(B/А) = 6/9 = 2/3.
Вероятность того, что третьим будет отобран мужчина, при условии, что уже отобраны двое мужчин, т.е. условная вероятность события С такова: P(C / АВ) = 5/8.
Искомая вероятность того, что все три отобранных лица окажутся мужчинами, P(ABC) = P(A) P(B / А) P(C / АВ) = 7/10 · 2/3 · 5/8 = 7/24.
