Статистическое определение вероятности используется в случае, когда исходы опыта не являются равновозможными.
Относительная частота события А определяется равенством:
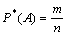 ,
,
где m – число испытаний, в которых событие А наступило, n – общее число произведенных испытаний.
Я. Бернулли доказал, что при неограниченном увеличении числа опытов относительная частота появления события будет практически сколь угодно мало отличаться от некоторого постоянного числа. Оказалось, что это постоянное число есть вероятность появления события. Поэтому, естественно, относительную частоту появления события при достаточно большом числе испытаний называть статистической вероятностью в отличие от ранее введенной вероятности.
Пример 1.8. Как приближенно установить число рыб в озере?
Пусть в озере х рыб. Забрасываем сеть и, допустим, находим в ней n рыб. Каждую из них метим и выпускаем обратно. Через несколько дней в такую же погоду и в том же месте забрасываем ту же самую сеть. Допустим, что находим в ней m рыб, среди которых k меченных. Пусть событие А – «пойманная рыба мечена». Тогда по определению относительной частоты  .
.
Но если в озере х рыб и мы в него выпустили n меченых, то 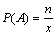 .
.
Так как Р *(А)» Р (А то ), 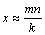 .
.