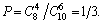Задача 1.1. Какова вероятность появления четного числа очков (событие А) при одном бросании игрального кубика?
Решение. Рассмотрим события Аi – выпало i очков, i = 1, 2, …,6. Очевидно, что эти события образуют схему случаев. Тогда число всех случаев n = 6. Выпадению четного числа очков благоприятствуют случаи А 2, А 4, А 6, т.е. m = 3. Тогда 
.
Задача 1.2. В урне 5 белых и 10 черных шаров. Шары тщательно перемешивают и затем наугад вынимают 1 шар. Какова вероятность того, что вынутый шар окажется белым?
Решение. Всего имеется 15 случаев, которые образуют схему случаев. Причем ожидаемому событию А – появлению белого шара, благоприятствуют 5 из них, поэтому 
.
Задача 1.3. Ребенок играет с шестью буквами азбуки: А, А, Е, К, Р, Т. Найти вероятность того, что он сможет сложить случайно слово КАРЕТА (событие А).
Решение. Решение осложняется тем, что среди букв есть одинаковые – две буквы «А». Поэтому число всех возможных случаев в данном испытании равно числу перестановок с повторениями из 6 букв:
.
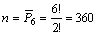Эти случаи равновозможны, попарно несовместны и образуют полную группу событий, т.е. образуют схему случаев. Лишь один случай благоприятствует событию А. Поэтому
.
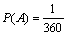Задача 1.4. Таня и Ваня договорились встречать Новый год в компании из 10 человек. Они оба очень хотели сидеть рядом. Какова вероятность исполнения их желания, если среди их друзей принято места распределять путем жребия?
Решение. Обозначим через А событие «исполнение желания Тани и Вани». 10 человек могут усесться за стол 10! разными способами. Сколько же из этих n = 10! равновозможных способов благоприятны для Тани и Вани? Таня и Ваня, сидя рядом, могут занять 20 разных позиций. В то же время восьмерка их друзей может сесть за стол 8! разными способами, поэтому m = 20∙8!. Следовательно,
.
Задача 1.5. Группа из 5 женщин и 20 мужчин выбирает трех делегатов. Считая, что каждый из присутствующих с одинаковой вероятностью может быть выбран, найти вероятность того, что выберут двух женщин и одного мужчину.
Решение. Общее число равновозможных исходов испытания равно числу способов, которыми можно выбрать трех делегатов из 25 человек, т.е.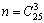 
. Подсчитаем теперь число благоприятствующих случаев, т.е. число случаев, при которых имеет место интересующее нас событие. Мужчина-делегат может быть выбран двадцатью способами. При этом остальные два делегата должны быть женщинами, а выбрать двух женщин из пяти можно 
. Следовательно, 
. Поэтому
.
Задача 1.6. Четыре шарика случайным образом разбрасываются по четырем лункам, каждый шарик попадает в ту или другую лунку с одинаковой вероятностью и независимо от других (препятствий к попаданию в одну и ту же лунку нескольких шариков нет). Найти вероятность того, что в одной из лунок окажется три шарика, в другой - один, а в двух остальных лунках шариков не будет.
Решение. Общее число случаев n =44. Число способов, которыми можно выбрать одну лунку, где будут три шарика, 
. Число способов, которыми можно выбрать лунку, где будет один шарик,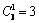 
. Число способов, которыми можно выбрать из четырех шариков три, чтобы положить их в первую лунку, 
. Общее число благоприятных случаев 
. Вероятность события: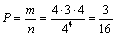 
Задача 1.7. В ящике 10 одинаковых шаров, помеченных номерами 1, 2, …, 10. На удачу извлечены шесть шаров. Найти вероятность того, что среди извлечённых шаров окажутся: а) шар №1; б) шары №1 и №2.
Решение. а) Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь шесть шаров из десяти, т.е.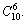 
Найдём число исходов, благоприятствующих интересующему нас событию: среди отобранных шести шаров есть шар №1 и, следовательно, остальные пять шаров имеют другие номера. Число таких исходов, очевидно, равно числу способов, которыми можно отобрать пять шаров из оставшихся девяти, т.е.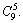 
Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов: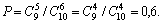 
б) Число исходов, благоприятствующих интересующему нас событию (среди отобранных шаров есть шары №1 и №2, следовательно, четыре шара имеют другие номера), равно числу способов, которыми можно извлечь четыре шаров из оставшихся восьми, т.е. 
Искомая вероятность 
