Если множество элементарных событий Ω={ω1,ω2,…ωN},конечно и все элементарные события равновозможны, то такая вероятностная схема носит название классической. В этом случае вероятность Р{А} наступления события А, состоящего из М элементарных событий, входящих в Ω, определяется как отношение числа М элементарных событий, благоприятствующих наступлению события А, к общему числу Nэлементарных событий. Эта формула носит название классической формулы вероятности: Р{А}= M/N.
В частности, согласно классической формуле вероятности:
Р{ωi }=1/N (i=1,2,..., N)
Р{Ω}= N/N =1
P{Æ}=0/N =0
"Вероятность случайного события";
Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий 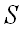 .
.
Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий 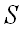 .
.
Случайным называют событие, которое при осуществлении определенной совокупности условий 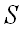 может либо произойти, либо не произойти.
может либо произойти, либо не произойти.
События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Два события называют совместными, если появление одного из них не исключает появление другого события в одном и том же испытании.
Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.
Элементарным исходом называется каждый из возможных результатов испытания.
Те элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию исходами.
Вероятностью события  называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Вероятность события  определяется формулой
определяется формулой
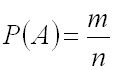 ,
,
где  – число элементарных исходов, благоприятствующих событию
– число элементарных исходов, благоприятствующих событию  , а
, а 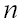 – число всех равновозможных несовместных элементарных исходов, образующих полную группу.
– число всех равновозможных несовместных элементарных исходов, образующих полную группу.
Свойства вероятности
1. Вероятность достоверного события равна единице.
2. Вероятность невозможного события равна нулю.
3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
 .
.
Вывод: вероятность любого события удовлетворяет двойному неравенству
 .
.
Относительной частотой события  называют отношение числа испытаний, в которых это событие появилось, к общему числу фактически произведенных испытаний.
называют отношение числа испытаний, в которых это событие появилось, к общему числу фактически произведенных испытаний.
Относительная частота события  определяется формулой
определяется формулой
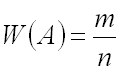 ,
,
где  – число испытаний, в которых событие
– число испытаний, в которых событие  появилось, а
появилось, а 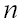 – общее число фактически произведенных испытаний.
– общее число фактически произведенных испытаний.
Основное отличие вероятности события от относительной частоты: вероятность вычисляют до опыта, а относительную частоту – после опыта.
Свойство устойчивости относительной частоты: если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота в этих опытах изменяется мало (тем меньше, чем больше число испытаний), причем она колеблется около некоторого постоянного числа – вероятности появления этого события.
Тема 1. Случайные события
1.1. Некоторые сведения из комбинаторики
1.1.1. Размещения
Рассмотрим простейшие понятия, связанные с выбором и расположением некоторого множества объектов.
Подсчет числа способов, которыми можно совершить эти действия, часто производится при решении вероятностных задач.
Определение. Размещением из n элементов по k (k ≤ n) называется любое упорядоченное подмножество из k элементов множества, состоящего из n различных элементов.
Пример. Следующие последовательности цифр являются размещениями по 2 элемента из 3 элементов множества {1;2;3}: 12, 13, 23, 21, 31, 32.
Заметим, что размещения отличаются порядком входящих в них элементов и их составом. Размещения 12 и 21 содержат одинаковые цифры, но порядок их расположения различен. Поэтому эти размещения считаются разными.
Число различных размещений из n элементов по k обозначается 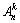 и вычисляется по формуле:
и вычисляется по формуле:
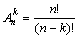 ,
,
где n! = 1∙2∙...∙(n - 1)∙ n (читается «n – факториал»).
Число двузначных чисел, которые можно составить из цифр 1, 2, 3 при условии, что ни одна цифра не повторяется равно: 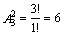 .
.

 .
. называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.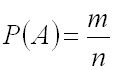 ,
, – число элементарных исходов, благоприятствующих событию
– число элементарных исходов, благоприятствующих событию 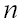 – число всех равновозможных несовместных элементарных исходов, образующих полную группу.
– число всех равновозможных несовместных элементарных исходов, образующих полную группу. .
. .
.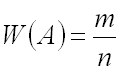 ,
,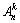 и вычисляется по формуле:
и вычисляется по формуле: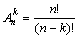 ,
,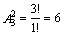 .
.


