Вероятность события – численная мера возможности его наступления.
Событие А называется благоприятствующим событию В, если всякий раз, когда наступает событие А, наступает и событие В.
События А 1, А 2,..., Аn образуют схему случаев, если они:
1) равновозможны;
2) попарно несовместны;
3) образуют полную группу.
В схеме случаев (и только в этой схеме) имеет место классическое определение вероятности P (A) события А. Здесь случаем называют каждое из событий, принадлежащих выделенной полной группе равновозможных и попарно несовместных событий.
Если n – число всех случаев в схеме, а m – число случаев, благоприятствующих событию А, то вероятность события А определяется равенством:
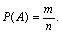
Из определения вероятности вытекают следующие ее свойства:
1. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый случай в схеме случаев благоприятствует событию. В этом случае m = n и, следовательно,

2. Вероятность невозможного события равна нулю.
Действительно, если событие невозможно, то ни один случай из схемы случаев не благоприятствует событию. Поэтому m =0 и, следовательно,

Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа случаев в схеме случаев. Поэтому 0< m < n, а, значит, 0< m / n <1 и, следовательно, 0 < P(A) < 1.
Итак, вероятность любого события удовлетворяет неравенствам
0 ≤ P(A) ≤ 1.
В настоящее время свойства вероятности определяются в виде аксиом, сформулированных А.Н. Колмогоровым.
Одним из основных достоинств классического определения вероятности является возможность вычислить вероятность события непосредственно, т.е. не прибегая к опытам, которые заменяют логическими рассуждениями.