Задача №8 3 страница
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ Задача 1. Виразити складні події
Зауваження. Вектор струму при проходженні схеми не може мати напрям справа наліво. 1.1.
Розв’язання Виразимо подію А через події Спосіб 1. Виходимо з того, що подія А є сумою наслідків, які їй сприяють, причому кожний із цих наслідків складається з 5 елементарних подій Маємо: Перший доданок справа в (А) означає, що всі 5 елементів схеми проводять струм, чотири наступних – усі елементи схеми, крім одного, проводять струм; чотири останніх – усі елементи схеми, крім двох, проводять струм. Наступне спрощення виразу для події А показано нижче у фігурних дужках. Букву А у виразі для спрощення і скорочення викладок опущено: ...
Спосіб 2. Проглядаємо схему зліва направо, враховуючи зауваження, і включаємо в подію А всі послідовності подій Маємо:
Спосіб 3. Виходимо з того, що схема проводить струм, якщо елементи: 1 або 2 і одночасно 3 або 4 та одночасно 5 проводять струм. А це згідно з означенням суми і добутку двох подій означає, що Виразимо подію
Можна використати формули (закон двоїстості) де Моргана: Відповідь: Зауваження. Відмітимо, що з розглянутих способів відшукування подій А і
1.2.
Розв’язання Спосіб 2
При спрощенні події Відповідь:
Зауваження. Розглянуті вище (при розв’язанні задачі 1.1.) 3 способи відшукання події А і Маємо:
Знайдемо також подію
Задача 2. В урні 10 куль (і – білих і (10 – і) – синіх). Із урни навмання способом
Додаткова інформація: а)
2.1 а) 4,5,4,5; б) 4,6,3,2,6. Розв’язання Подамо коротко умову першої задачі а): Нехай
де
i т.д. вiдповiдно,
i т.д. Точка у доданках в Ураховуючи тепер, що доданки в другій – залежні, маємо
або
Подамо коротко умову другої задачі б):
де, наприклад,
вiдповiдно
або
Зауваження. Вище, при обчисленні
де
Відповідь:
Задача 3. Точку кидають на площину Додаткова інформація:
3.1.
Розв’язання Перша подвійна нерівність задає смугу між паралельними прямими
друга – між паралельними прямими
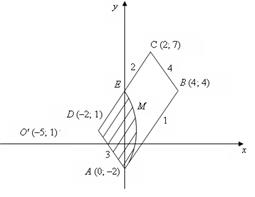
Отже, вершини А, В, С, D паралелограма, заданого двома зазначеними нерівностями, знайдемо, розв’язуючи такі системи рівнянь:
Таким чином, А = А (0; – 2), В = В (4; 4), С = С (2; 7), D = D (– 2; 1). Наносимо на площині знайдені вершини паралелограма і будуємо сам паралелограм (область Остання нерівність задає підобласть
Таким чином, розглядувана крива – коло з центром у точці Знайдемо точку перетину кола зі сторонами
Таким чином, А = А (0; – 2). Друга точка лежить за межами області
Таким чином, Е = Е (0; 4). Друга точка лежить за межами області Наприклад, точка
Отже, підобласть
то дуга кола пряму Зображуємо область Згідно з формулою геометричної ймовірності маємо
де т – площа. Шукаємо
Тоді:
Отже, Відповідь: 3.2. Розв’язання
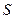 , задана нерівністю , задана нерівністю 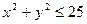 , є кругом, обмеженим колом радіусом 5 із центром на початку координат. Підобласть , є кругом, обмеженим колом радіусом 5 із центром на початку координат. Підобласть 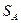 області області 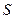 задана подвійною нерівністю задана подвійною нерівністю
Це розміщена всередині круга область між прямими
Прямі на площині
Таким чином,
Таким чином, Зображуємо області
Отже,
Відповідь:
Задача 4. Є три урни, в кожній з яких по 10 куль – білих і синіх. Дії з кулями виконуються відповідно до схеми і навмання. Необхідно: 1) знайти ймовірність того, що результатом останньої дії буде біла куля; 2) знайти післядослідні ймовірності заданих гіпотез. Додаткова інформація: схема (починає кожний рядок і одна для всіх варіантів рядка. Цифри в рядку на схемі – номери урн, над рисками – кількість куль, що перекладаються); кількість білих куль в урнах; гіпотези. Hij (i=1,2; j= Ні1 – 2 білі кулі; Ні2 – 1 біла і 1 синя кулі; Н і3 – 2 сині кулі; Ні4 – принаймні 1 біла куля; Ні5 – принаймні 1 синя куля; Ні6 – 2 білі або 2 сині кулі. 4.1. 3 2 2, 1 2 3, 3 1 ; 6, 4, 9; Н 11, Н 26. Розв’язання Подамо схему у більш наочному вигляді:
1. Нехай А – результатом останньої дії буде біла куля. Подія А настає лише за умови настання однієї з гіпотез Ні – у діях 1,2 перекладалася і – та комбінація з чотирьох куль. Нехай В – перекладалася біла куля; S – перекладалася синя куля. Тоді:
|

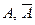 через елементарні події
через елементарні події 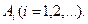 А – схема проводить струм,
А – схема проводить струм, 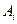
 –
– - й елемент схеми проводить струм.
- й елемент схеми проводить струм.
 .
.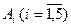 .
.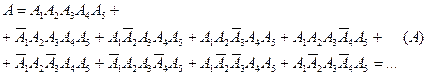
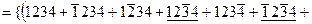

 .
.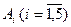 , які приводять до “успіху”.
, які приводять до “успіху”.
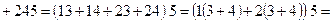
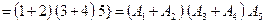 .
.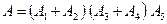 .
.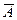 через подію
через подію 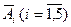 . Це можна зробити способами 1 - 3. Наприклад, способом 2. Проглядаємо схему зліва направо і включаємо в подію
. Це можна зробити способами 1 - 3. Наприклад, способом 2. Проглядаємо схему зліва направо і включаємо в подію 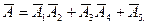
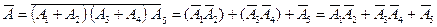 .
.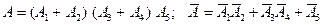 .
.
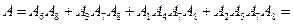
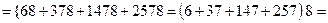
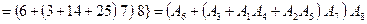 ,
,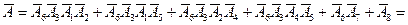
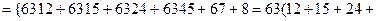
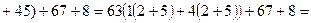
 .
.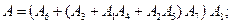
 .
.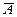 , як правило, не вичерпують усі можливості. Наприклад, задачу 1.2 доцільно розв’язувати, комбінуючи способи 2 і 3.
, як правило, не вичерпують усі можливості. Наприклад, задачу 1.2 доцільно розв’язувати, комбінуючи способи 2 і 3.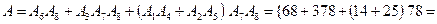

 .
.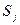 виймають кулі. Знайти ймовірність того, що серед вийнятих куль
виймають кулі. Знайти ймовірність того, що серед вийнятих куль 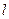 білих.
білих.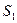 –
– 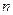 разів виймають по одній кулі і повертають її назад;
разів виймають по одній кулі і повертають її назад; –
– 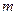 куль і повертають їх назад;
куль і повертають їх назад;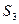 – виймають
– виймають 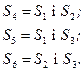
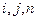 (або
(або 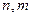 ),
), 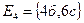 ;
;  4 рази виймають по одній кулі і повертають її назад і виймають 4 кулі, не повертаючи їх назад;
4 рази виймають по одній кулі і повертають її назад і виймають 4 кулі, не повертаючи їх назад; 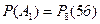 – необхідно знайти.
– необхідно знайти.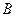 – у випробуванні вийнято білу кулю, тоді подію
– у випробуванні вийнято білу кулю, тоді подію 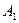 – подію, задану умовою а) задачі, можна подати у вигляді
– подію, задану умовою а) задачі, можна подати у вигляді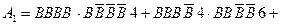


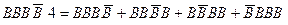

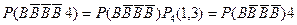
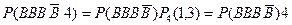
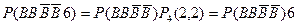

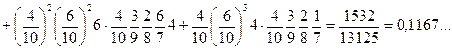
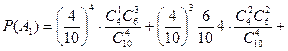
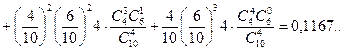 .
.
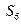 – 3 рази виймають по 2 кулі і повертають їх назад і виймають 3 кулі, не повертаючи їх назад;
– 3 рази виймають по 2 кулі і повертають їх назад і виймають 3 кулі, не повертаючи їх назад; 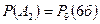 – необхідно знайти.
– необхідно знайти.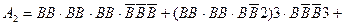
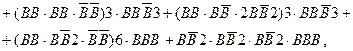

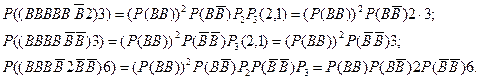 Ураховуючи тепер, що доданки в
Ураховуючи тепер, що доданки в 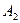 несумiснi, множники у них незалежнi i що в першiй серiї пари випробувань незалежні, але випробування у парах залежні, а в другій – залежні, маємо
несумiснi, множники у них незалежнi i що в першiй серiї пари випробувань незалежні, але випробування у парах залежні, а в другій – залежні, маємо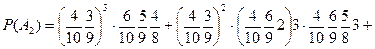

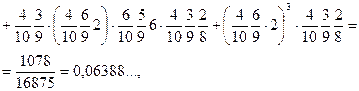

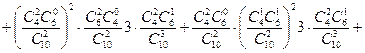

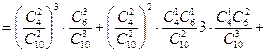
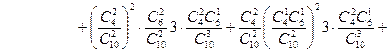
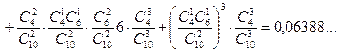
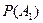 і
і 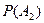 другим способом, обчислення ймовірності добутку залежних подій виконувалося за формулою
другим способом, обчислення ймовірності добутку залежних подій виконувалося за формулою ,
,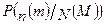 – ймовірність того, що в
– ймовірність того, що в 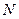 (залежних) випробуваннях вона настане рівно
(залежних) випробуваннях вона настане рівно 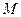 разів.
разів.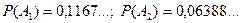
 в область
в область 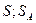 .
.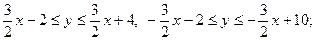
 .
.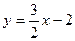 і
і 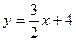 ,
,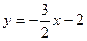 і
і  .
.


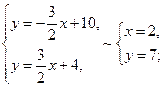


 .
.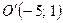 і радіусом
і радіусом 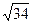 .
.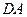 і
і 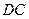 паралелограма. Для цього розв’яжемо такі системи рівнянь:
паралелограма. Для цього розв’яжемо такі системи рівнянь:

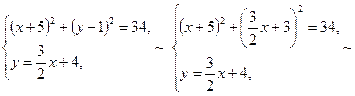
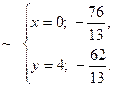
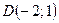 задовольняє нерівність
задовольняє нерівність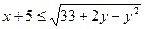 .
.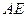 кола, і оскільки
кола, і оскільки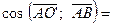
 АВ
АВ 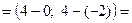
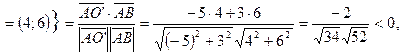
 не перетинає.
не перетинає. .
.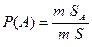 ,
, і
і  .Ураховуючи симетрію
.Ураховуючи симетрію 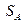 відносно осі
відносно осі 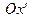 , яка проходить через точку
, яка проходить через точку 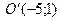 паралельно осі
паралельно осі 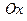 , рівняння кола, що є частиною межі
, рівняння кола, що є частиною межі  в області
в області 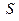 , запишемо відносно нової системи координат
, запишемо відносно нової системи координат  .Маємо
.Маємо
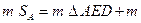 сегмента
сегмента 

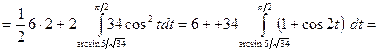
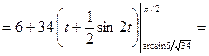
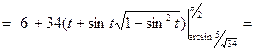
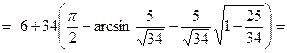
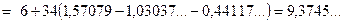 ,
,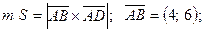
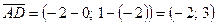 ,
,
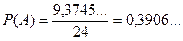

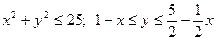 .
.
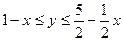 .
. і
і 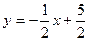 .
.
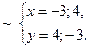
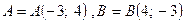 .
.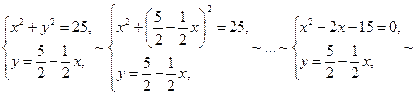
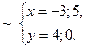
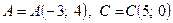 .
.
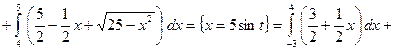
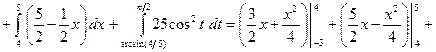

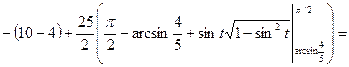
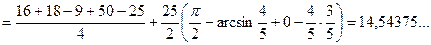 ,
,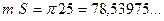
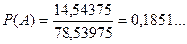
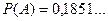
 ) – в дії і перекладалися:
) – в дії і перекладалися:
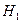 =
=  P (
P (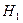 )=
)= 
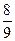
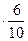
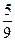 =
=  , P (
, P ( )=
)= 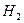 =
= 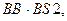 P (
P ( 2 =
2 =  , P (
, P (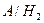 )=
)= 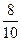 ,
,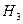 =
= 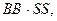 P (
P (
 =
= 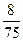 , P (
, P (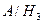 )=
)=  ,
,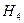 =
= 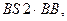 P (
P (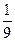 2
2 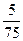 , P (
, P (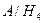 )=
)= 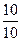 ,
,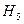 =
=  P (
P (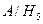 )=
)= 


