Задача №8 5 страница
0 2 3 x

y = f (x)
0 1 2 3 x
б) Шукаємо числові характеристики випадкової величини X:
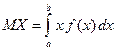 , ,
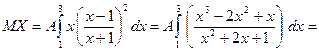
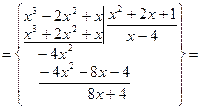 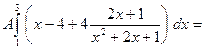
 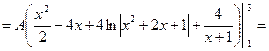 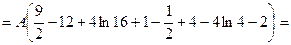  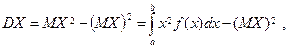  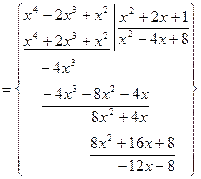 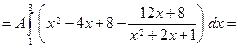
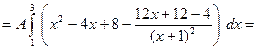
 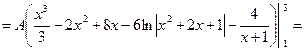
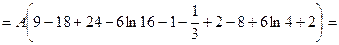
 , ,
 , ,
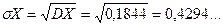
Шукаємо ймовірність 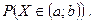
 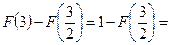
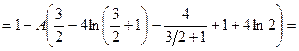
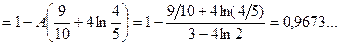
Відповідь: 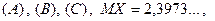
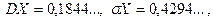 
Задача 8. З продукції автомата було зроблено вибірку об’ємом 300 валиків. Параметром Х, що контролюється, є відхилення діаметра валика від номінального розміру (мм). Нижче подано отриманий розподіл частот. Необхідно:
1. Побудувати гістограму відносних частот і емпіричну функцію розподілу вибірки.
2. Обчислити числові характеристики вибірки 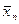 : :  , ,  , , 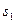 . .
3. За виглядом гістограми з урахуванням отриманих числових характеристик вибрати модель закону розподілу і при рівні значущості  перевірити зроблене припущення (відносно моделі закону розподілу) за допомогою критерію Пірсона. На гістограму відносних частот накласти графік щільності вибраного теоретичного закону розподілу. перевірити зроблене припущення (відносно моделі закону розподілу) за допомогою критерію Пірсона. На гістограму відносних частот накласти графік щільності вибраного теоретичного закону розподілу.
4. З надійністю  знайти надійні інтервали для математичного сподівання і дисперсії генеральної сукупності Х. знайти надійні інтервали для математичного сподівання і дисперсії генеральної сукупності Х.
| (ai - 1; ai)
| (– 0,15; – 0,13)
| (– 0,13; – 0,11)
| (– 0,11; – 0,09)
| (– 0,09; – 0,07)
| (– 0,07; – 0,05)
| (– 0,05; – 0,03)
| (– 0,03; – 0,01)
| (– 0,01; 0,01)
| (0,01; 0,03)
| (0,03; 0,05)
| (0,05; 0,07)
| (0,07; 0,09)
| (0,09; 0,11)
| (0,11; 0,13)
| (0,13; 0,15)
| | ni
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Зауваження. Якщо номер варіанта розрахункової роботи: непарний і не кратний 3, то  , парний і не кратний 3, то , парний і не кратний 3, то  , і кратний 3, то , і кратний 3, то 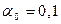 . .
Розв’язання
1. Будуємо гістограму відносних частот (рис. 1.1) необхідну для цього інформацію вносимо в таблицю 1.1 (п’ять перших стовпців).
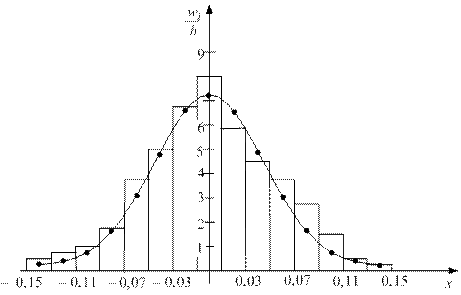 Рис. 1.1 Рис. 1.1
 Рис. 1. 2 Рис. 1. 2
5. Будуємо емпіричну функцію розподілу вибірки (рис. 1. 2):
6. 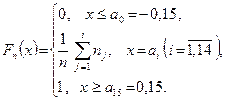
7. Обчислювану інформацію вносимо в таблицю 1.1 (шостий і сьомий cтовпці).
Таблиця 3.1

| 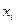
| 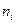
| 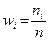
| 
| 
| 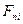
| 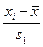
| 
| |
| – 0,14
|
| 3/300
| 3/6 = 0,5
| – 0,13
| 0,01
| – 2,54
| 0,29
| |
| – 0,12
|
| 5/300
| 5/6 = 0,8 3
| – 0,11
| 0,03
| – 2,18
| 0,67
| |
| – 0,10
|
| 8/300
| 8/6 = 1, 3
| – 0,09
| 0,05
| – 1,82
| 1,38
| |
| – 0,08
|
| 13/300
| 13/6 = 2,1 6
| – 0,07
| 0,10
| – 1,45
| 2,52
| |
| – 0,06
|
| 25/300
| 25/6 = 4,1 6
| – 0,05
| 0,18
| – 1,09
| 3,98
| |
| – 0,04
|
| 31/300
| 31/6 = 5,1 6
| – 0,03
| 0,28
| – 0,73
| 5,53
| |
| – 0,02
|
| 42/300
| 42/6 = 7
| – 0,01
| 0,42
| – 0,37
| 6,74
| |
|
|
| 50/300
| 50/6 = 8, 3
| 0,01
| 0,59
|
| 7,21
| |
| 0,02
|
| 37/300
| 37/6 = 6,1 6
| 0,03
| 0,71
| 0,35
| 6,78
| |
| 0,04
|
| 27/300
| 27/6 = 4,5
| 0,05
| 0,82
| 0,72
| 5,57
| |
| 0,06
|
| 24/300
| 24/6 = 4
| 0,07
| 0,88
| 1,08
| 4,03
| |
| 0,08
|
| 18/300
| 18/6 = 3
| 0,09
| 0,94
| 1,44
| 2,56
| |
| 0,10
|
| 11/300
| 11/6 =1,8 3
| 0,11
| 0,98
| 1,80
| 1,43
| |
| 0,12
|
| 4/300
| 4/6 = 0, 6
| 0,13
| 0,99
| 2,16
| 0,70
| |
| 0,14
|
| 2/300
| 2/6 = 0, 3
| 0,15
|
| 2,52
| 0,30
|
Примітка. У таблиці 1.1
 , , 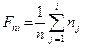 . .
2. Обчислюємо числові характеристики вибірки  : : 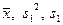 : : 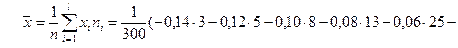 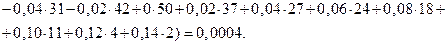 вреOскільки n = 300 > 30, то вреOскільки n = 300 > 30, то  . пар . пар 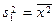   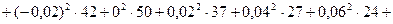  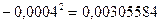 ; ; 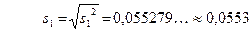 . .
3.Покладаємо, що 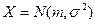 , і перевіряємо зроблене припущення за допомогою критерію Пірсона: пііп3.1. , і перевіряємо зроблене припущення за допомогою критерію Пірсона: пііп3.1.  вчп3.2. вчп3.2.  , рррвпапаап , рррвпапаап 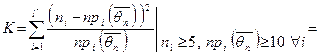  ііівп ііівп 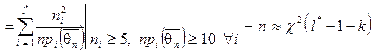 , ,
де l* – нове, зменшене порівняно з l, число підінтервалів розбиття інтервалу(a, b), отримане об’єднанням сусідніх підінтервалів з метою задоволення умов 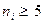 , ,  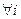 . При цьому . При цьому 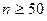 (див. табл. 1. 2); (див. табл. 1. 2); 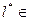 [7, l); [7, l);
l – задане умовою число підінтервалів  , , 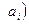  , , 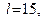 розбиття інтервалу розбиття інтервалу 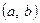 множини значень випадкової величини X інтервалу множини значень випадкової величини X інтервалу  точками точками    ; ;
 – емпіричні частоти; – емпіричні частоти;
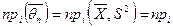 – теоретичні частоти; – теоретичні частоти;
k – число невідомих параметрів розподілу  , , 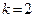 ; ;
   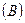
причому, оскільки нормальний розподіл визначений при 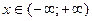 , то , то  , ,  . .
3.3. 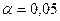 . .
3.4.
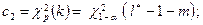
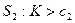 . .
3.5. Обчислюємо реалізацію статистики критерію 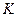 , за формулою (А), вносимо в таблицю 1.2. , за формулою (А), вносимо в таблицю 1.2.
 ; ;
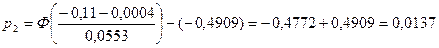 ; ;
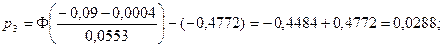
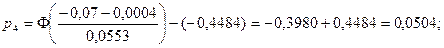
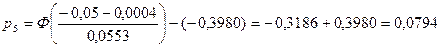 ; ;
 ; ;
 ; ;
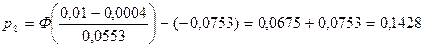 ; ;
 ; ;
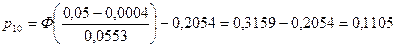 ; ;
 ; ;
 ; ;
 ; ;
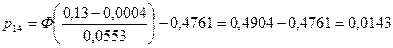 ; ;
 . .
Таблиця 1.2
|
i
| 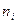
| 
| 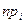
| 
| |
| 
| 0,0091
| 
| 16,537
| |
| 0,0137
| |
| 0,0288
| |
|
| 0,0504
| 15,12
| 11,177
| |
|
| 0,0794
| 23,82
| 26,238
| |
|
| 0,1098
| 32,94
| 29,174
| |
|
| 0,1335
| 40,05
| 44,045
| |
|
| 0,1428
| 42,84
| 58,357
| |
|
| 0,1379
| 41,37
| 33,092
| |
|
| 0,1105
| 33,15
| 21,991
| |
|
| 0,0803
| 24,09
| 23,910
| |
|
| 0,0512
| 15,36
| 21,094
| |
| 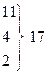
| 0,0287
| 
| 18,314
| |
| 0,0143
| |
| 0,0096
| |
|
| 1,0000
| 300,00
| k = 303,932 – – 300 = 3,932
| Таким чином, 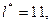 тоді тоді
 = =
= 15,51 (табл. 4);
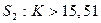 . .
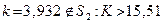 , отже, гіпотезу про нормальний розподіл генеральної сукупності , отже, гіпотезу про нормальний розподіл генеральної сукупності 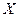 приймаємо. приймаємо.
3.6. На гістограму відносних частот накладаємо графік щільності вибраного теоретичного (нормального) закону розподілу:
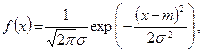
де замість параметрів 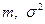 використовуються їх вибіркові оцінки використовуються їх вибіркові оцінки  і і  . Отже, при побудові кривої . Отже, при побудові кривої 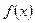 використовуємо таблицю щільності ймовірностей стандартного нормального розподілу у відповідності до формули використовуємо таблицю щільності ймовірностей стандартного нормального розподілу у відповідності до формули
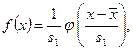
враховуючи, що функція 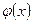 є парною. Обчислену інформацію розміщуємо в таблиці 1.1 (два останніх стовпці). є парною. Обчислену інформацію розміщуємо в таблиці 1.1 (два останніх стовпці).
Зауваження. Відмітимо, що теоретичні частоти  ми шукали вище, обчислюючи ймовірності ми шукали вище, обчислюючи ймовірності  за формулою (В), тобто використовуючи функцію розподілу за формулою (В), тобто використовуючи функцію розподілу
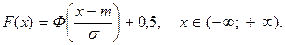
Ті самі ймовірності можна обчислити, використовуючи щільність розподілу
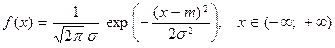
за формулою
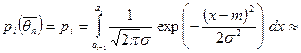
(згідно з теоремою про середнє для визначеного інтеграла)
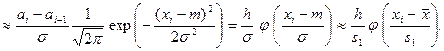
Відповідні обчислення подано в таблиці 1.3.
4. Шукаємо надійні інтервали для невідомих параметрів 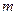 і і  нормальної генеральної сукупності. нормальної генеральної сукупності.
Таблиця 1.3
| i
| 
| 
| 
| 
| 
| 
| |
|
|
|
| 0,0032
| 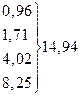
| 17,135
| |
| 
| – 0,14
| 0,0158
| 0,0057
| |
| – 0,12
| 0,0371
| 0,0134
| |
| – 0,10
| 0,0761
| 0,0275
| |
|
| – 0,08
| 0,1394
| 0,0504
| 15,12
| 11,177
| |
|
| – 0,06
| 0,2203
| 0,0797
| 23,91
| 26,140
| |
|
| – 0,04
| 0,3056
| 0,1105
| 33,15
| 28,989
| |
|
| – 0,02
| 0,3726
| 0,1348
| 40,44
| 43,620
| |
|
|
| 0,3989
| 0,1443
| 43,29
| 57,750
| |
|
| 0,02
| 0,3752
| 0,1357
| 40,71
| 33,628
| |
|
| 0,04
| 0,3079
| 0,1113
| 33,39
| 21,833
| |
|
| 0,06
| 0,2227
| 0,0805
| 24,15
| 23,851
| |
|
| 0,08
| 0,1415
| 0,0512
| 15,36
| 21,094
| |
| 
| 0,10
| 0,0790
| 0,0286
| 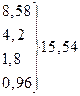
| 18,597
| |
| 0,12
| 0,0387
| 0,0140
| |
| 0,14
| 0,0167
| 0,0060
| |
|
|
|
| 0,0032
| |
|
|
|
| 1,0000
|
|  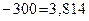
| Примітка. У таблиці 1.3
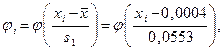
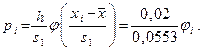
А перший і останній (неповні) рядки таблиці враховують, що нормальний розподіл визначений при 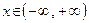 і що і що  повинна дорівнювати одиниці. повинна дорівнювати одиниці.
4.1.
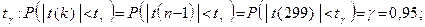
 (табл. 9), (табл. 9),
або
 (табл. 5). (табл. 5).
Отже, при невідомому  невідоме математичне сподівання невідоме математичне сподівання 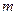 із надійністю із надійністю 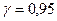 покриває інтервал покриває інтервал
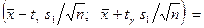
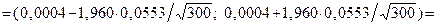
 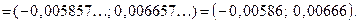
4.2. При  квантиль квантиль 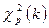 розподілу розподілу  можна знайти за формулою можна знайти за формулою
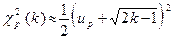 , ,
де  квантиль стандартного нормального розподілу квантиль стандартного нормального розподілу  . .
Таким чином,
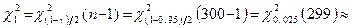
 { { 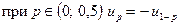 }= }=
 {з табл. 3 {з табл. 3 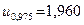 }= }=
 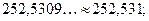
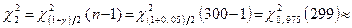
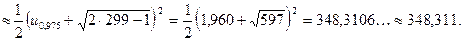
Отже, при невідомому 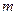 невідоме невідоме  із надійністю із надійністю 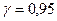 покриває інтервал покриває інтервал
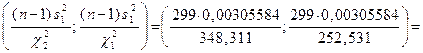

Задача 9. Два підприємства виробляють дріт: 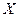 – міцність на розрив (кг/мм2) дроту, виготовленого на підприємстві – міцність на розрив (кг/мм2) дроту, виготовленого на підприємстві  , ,  – міцність на розрив дроту, виготовленого на підприємстві – міцність на розрив дроту, виготовленого на підприємстві 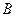 . Можна вважати . Можна вважати 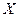 і і  нормально розподіленими і незалежними, а також, що нормально розподіленими і незалежними, а також, що 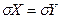 . З кожного підприємства було відібрано і перевірено дріт з 10 котушок. Результати перевірки подано нижче. Необхідно: . З кожного підприємства було відібрано і перевірено дріт з 10 котушок. Результати перевірки подано нижче. Необхідно:

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Влияние первой русской революции 1905-1907 гг. на Казахстан. Революция в России (1905-1907 гг.), дала первый толчок политическому пробуждению трудящихся Казахстана, развитию национально-освободительного рабочего движения против гнета. В Казахстане, находившемся далеко от политических центров Российской империи...
Виды сухожильных швов После выделения культи сухожилия и эвакуации гематомы приступают к восстановлению целостности сухожилия...
КОНСТРУКЦИЯ КОЛЕСНОЙ ПАРЫ ВАГОНА Тип колёсной пары определяется типом оси и диаметром колес. Согласно ГОСТ 4835-2006* устанавливаются типы колесных пар для грузовых вагонов с осями РУ1Ш и РВ2Ш и колесами диаметром по кругу катания 957 мм. Номинальный диаметр колеса – 950 мм...
|
Общая и профессиональная культура педагога: сущность, специфика, взаимосвязь Педагогическая культура- часть общечеловеческих культуры, в которой запечатлил духовные и материальные ценности образования и воспитания, осуществляя образовательно-воспитательный процесс...
Устройство рабочих органов мясорубки Независимо от марки мясорубки и её технических характеристик, все они имеют принципиально одинаковые устройства...
Ведение учета результатов боевой подготовки в роте и во взводе Содержание журнала учета боевой подготовки во взводе. Учет результатов боевой подготовки - есть отражение количественных и качественных показателей выполнения планов подготовки соединений...
|
|





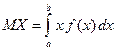 ,
,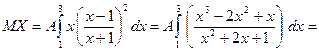
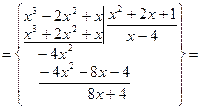


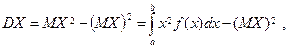

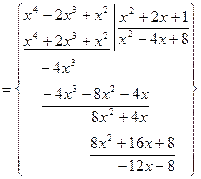
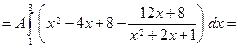
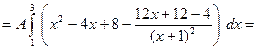

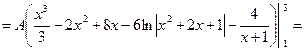
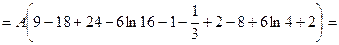
 ,
, ,
,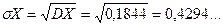
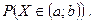

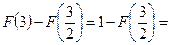
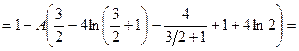
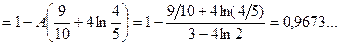
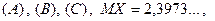
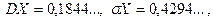

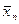 :
:  ,
,  ,
, 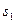 .
. перевірити зроблене припущення (відносно моделі закону розподілу) за допомогою критерію Пірсона. На гістограму відносних частот накласти графік щільності вибраного теоретичного закону розподілу.
перевірити зроблене припущення (відносно моделі закону розподілу) за допомогою критерію Пірсона. На гістограму відносних частот накласти графік щільності вибраного теоретичного закону розподілу. знайти надійні інтервали для математичного сподівання і дисперсії генеральної сукупності Х.
знайти надійні інтервали для математичного сподівання і дисперсії генеральної сукупності Х. , парний і не кратний 3, то
, парний і не кратний 3, то  , і кратний 3, то
, і кратний 3, то 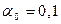 .
.  Рис. 1.1
Рис. 1.1 Рис. 1. 2
Рис. 1. 2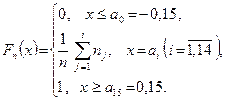

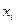
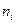
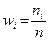


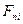
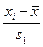

 ,
, 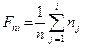 .
. :
: 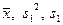 :
: 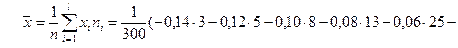
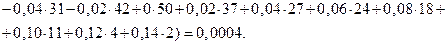 вреOскільки n = 300 > 30, то
вреOскільки n = 300 > 30, то  . пар
. пар 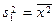


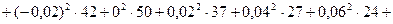

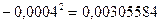 ;
; 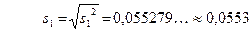 .
.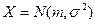 , і перевіряємо зроблене припущення за допомогою критерію Пірсона: пііп3.1.
, і перевіряємо зроблене припущення за допомогою критерію Пірсона: пііп3.1.  вчп3.2.
вчп3.2.  , рррвпапаап
, рррвпапаап 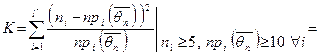
 ііівп
ііівп 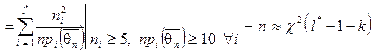 ,
,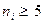 ,
, 
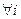 . При цьому
. При цьому 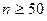 (див. табл. 1. 2);
(див. табл. 1. 2); 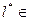 [7, l);
[7, l); ,
, 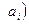
 ,
, 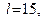 розбиття інтервалу
розбиття інтервалу 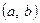 множини значень випадкової величини X інтервалу
множини значень випадкової величини X інтервалу  точками
точками 

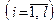 ;
;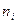 – емпіричні частоти;
– емпіричні частоти;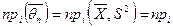 – теоретичні частоти;
– теоретичні частоти; ,
, 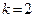 ;
;


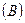
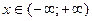 , то
, то  ,
,  .
.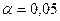 .
.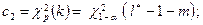
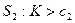 .
.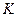 , за формулою (А), вносимо в таблицю 1.2.
, за формулою (А), вносимо в таблицю 1.2. ;
;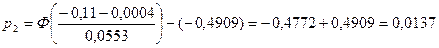 ;
;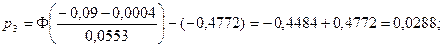
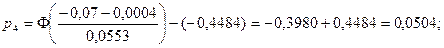
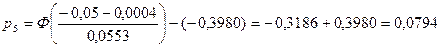 ;
; ;
; ;
;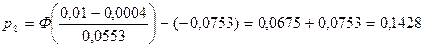 ;
; ;
;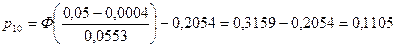 ;
; ;
; ;
; ;
;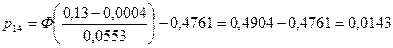 ;
; .
.
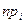



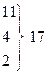

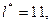 тоді
тоді =
=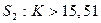 .
.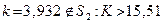 , отже, гіпотезу про нормальний розподіл генеральної сукупності
, отже, гіпотезу про нормальний розподіл генеральної сукупності 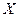 приймаємо.
приймаємо.
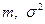 використовуються їх вибіркові оцінки
використовуються їх вибіркові оцінки  і
і  . Отже, при побудові кривої
. Отже, при побудові кривої 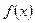 використовуємо таблицю щільності ймовірностей стандартного нормального розподілу у відповідності до формули
використовуємо таблицю щільності ймовірностей стандартного нормального розподілу у відповідності до формули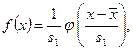
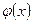 є парною. Обчислену інформацію розміщуємо в таблиці 1.1 (два останніх стовпці).
є парною. Обчислену інформацію розміщуємо в таблиці 1.1 (два останніх стовпці). ми шукали вище, обчислюючи ймовірності
ми шукали вище, обчислюючи ймовірності  за формулою (В), тобто використовуючи функцію розподілу
за формулою (В), тобто використовуючи функцію розподілу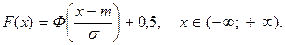
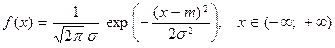
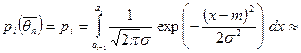
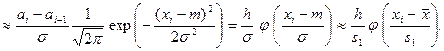
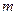 і
і  нормальної генеральної сукупності.
нормальної генеральної сукупності.


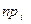
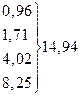


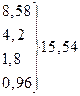

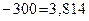
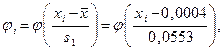
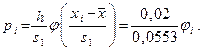
 і що
і що  повинна дорівнювати одиниці.
повинна дорівнювати одиниці.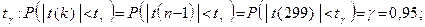
 (табл. 9),
(табл. 9), (табл. 5).
(табл. 5).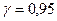 покриває інтервал
покриває інтервал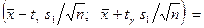
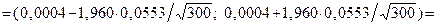

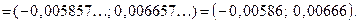
 квантиль
квантиль 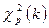 розподілу
розподілу  можна знайти за формулою
можна знайти за формулою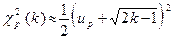 ,
, квантиль стандартного нормального розподілу
квантиль стандартного нормального розподілу  .
.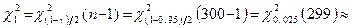
 {
{ 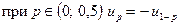 }=
}= {з табл. 3
{з табл. 3 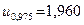 }=
}=
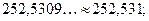
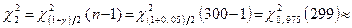
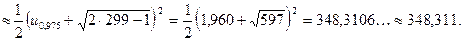
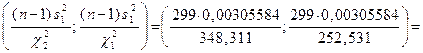

 ,
,  – міцність на розрив дроту, виготовленого на підприємстві
– міцність на розрив дроту, виготовленого на підприємстві 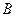 . Можна вважати
. Можна вважати 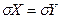 . З кожного підприємства було відібрано і перевірено дріт з 10 котушок. Результати перевірки подано нижче. Необхідно:
. З кожного підприємства було відібрано і перевірено дріт з 10 котушок. Результати перевірки подано нижче. Необхідно:


