Задача №8 4 страница
Вище, у першому стовпці, гіпотези Тоді згідно з формулою повної ймовірності P (A) = маємо P (A) = 2. Згідно з формулами Байєса, враховуючи зміст гіпотез
Відповідь: P (A)=
4.2. 3 2 2, 2 2 1, 2 1 , 6,10,7; Розв’язання
1. А – результатом останньої дії буде біла куля; Ні – у діях 1,2 перекладалася і -та комбінація з чотирьох куль; В – перекладалася біла куля; S – перекладалася синя куля.
2. Ураховуючи зміст гіпотез H 12 і H 23 , маємо P = P Відповідь: P (A) = P Задача 5. Знайти ймовірність того, що в n незалежних випробуваннях подія А настане рівно М разів, якщо ймовірність настання А в кожному з них однакова і дорівнює р. Додаткова інформація. а) n; M; p, б) n; M; p.
5.1. a) 8; не менше 2 і менше 6; 0,01; б) 300; менше 71; 0,2. Розв’язання Нехай А – подія, задана умовою а); В – подія, задана умовою б). Тоді: а) ймовірність Р (А), ураховуючи відносно невелике n, шукаємо, використовуючи формулу Бернуллі, точніше одну з її властивостей: P (A)= Маємо: P (A)= = = = +
б) ймовірність Р (В) шукаємо, використовуючи інтегральну теорему Муавра-Лапласа: Pn (а, b) Маємо: P (B)= P 300(0; 70)
Відповідь: Р (А) = 0,002690..., Р (В) = 0,9251.
5.2. а) 300; 2 або 3; 0,01; б) 300; більше 190 і не більше 193; 0,6. Розв’язання Нехай А – подія, задана умовою а); В – подія, задана умовою б). а) оскільки р = 0,01 < 0,1 і npq = ймовірність Р (А) шукаємо за формулою Пуассона:
Маємо:
б) ймовірність Р (В), оскільки р = 0,6 > 0,5 і npq =
Маємо:
Відповідь: Р (А) = 0,4480..., Р (В) = 0,05218...
Задача 6. Дискретна випадкова величина Додаткова інформація: зв’язок між ймовірностями (дві рівності);
6.1. Розв’язання 1. Шукаємо закон розподілу дискретної випадкової величини X у вигляді X P
Невідомі ймовірності шукаємо як розв’язок системи
Спочатку запишемо її у стандартній формі
А тепер розв’язуємо за допомогою формул Крамера, матричним способом, методом Гауса або методом Жордана – Гауса (якимось одним). Наприклад, методом Жордана – Гауса:
Таким чином, Невідомі
~ Порівняно із системою відносно З першого рівняння маємо
З другого рівняння:
Підставимо спочатку
Отже,
Умову задачі X – 2 4 7 P 0,1 0,6 0,3. (А) 2. Знайдемо функцію розподілу
Графік F (x)має вигляд
– 2 1 4 7 x 3. Відповідь: (А), (В), Р (
Задача 7. Дана рівність, яка на заданому проміжку визначає функцію (щільність) розподілу неперервної випадкової величини X. Необхідно: а) знайти параметр Додаткова інформація: 7.1. Розв’язання а) Параметр А шукаємо з умови, що
Отже,
Знайдемо щільність розподілу
Отже,
Графіки F (x) і f (x) мають такий вигляд:
y = F (x)   
1 2 3 x (C)
f(x)

 
    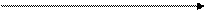
0 2 3 x
б) Шукаємо числові характеристики випадкової величини X:
Шукаємо ймовірність
=
Відповідь:
7.2. Розв’язання а) Параметр А шукаємо з умови
Маємо:
звідки
Отже,
Знаходимо функцію розподілу F (x), використовуючи співвідношення
Отже,
Графіки F (x) і f (x) мають вигляд
у y = F (x)   
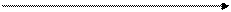 
|

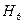 =
=  P (
P (
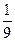 2
2 
 =
= 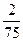 , Р (
, Р (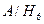 )=
)= 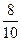 .
.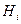 (і =
(і =  ) подано як комбінації елементарних подій. Точка у виразі справа відокремлює першу і другу дії; BS 2 = BS + SB, оскільки події BS i SB мають однакову ймовірність. У другому стовпці подано ймовірності гіпотез P (
) подано як комбінації елементарних подій. Точка у виразі справа відокремлює першу і другу дії; BS 2 = BS + SB, оскільки події BS i SB мають однакову ймовірність. У другому стовпці подано ймовірності гіпотез P (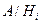 ) (і =
) (і = 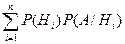
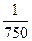 (
(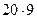 +
+ 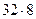 +
+  +
+  +
+ 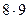 +
+ 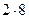 ) =
) =  .
.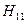 і
і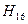 , маємо
, маємо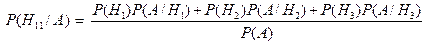 =
= =
= 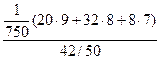 =
=  ,
,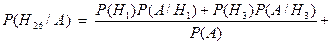
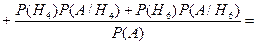
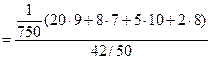 =
=  .
.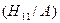 =
= 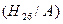 =
=  ,
, 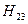 .
.
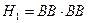 , P (
, P (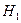 ) =
) =  , P
, P 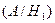 =
= 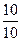 ,
, , P (
, P (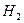 )=
)= 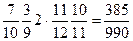 , P
, P 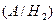 =
= 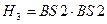 , P (
, P ( )=
)= 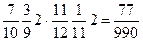 , P
, P  =
= 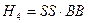 , P (
, P ( ) =
) = 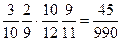 , P
, P  =
= 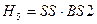 , P (
, P (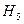 )=
)=  , P
, P  =
= 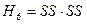 , P (
, P ( ) =
) =  , P
, P 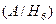 =
= 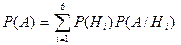 =
=  =
= 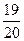 .
.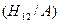 =
=  =
=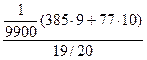 =
=  ,
,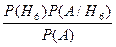 =
=  =
= 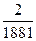 .
.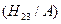 =
=  =
=  .
.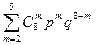 =
=
 =
=

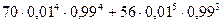 =0,002690…;
=0,002690…;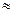
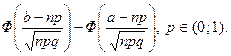
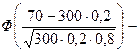
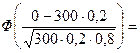
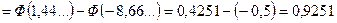 .
.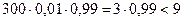 ,
,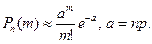

 ,
, , шукаємо за формулою Муавра –Лапласа
, шукаємо за формулою Муавра –Лапласа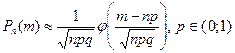 .
.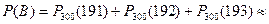
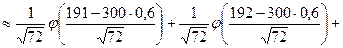
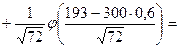
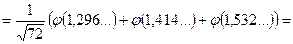


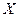 має лише 3 значення
має лише 3 значення 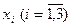 , причому
, причому 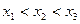 і
і  . Відомі зв’язок між ймовірностями
. Відомі зв’язок між ймовірностями 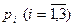 , заданий двома рівностями, і числові характеристики
, заданий двома рівностями, і числові характеристики 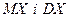 . Знайти: 1) закон розподілу
. Знайти: 1) закон розподілу  і побудувати її графік; 3) ймовірність Р(
і побудувати її графік; 3) ймовірність Р(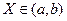 ).
).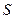 ;
; 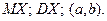
 .
.
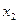
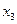


 .
.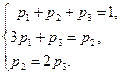

 шукаємо із системи
шукаємо із системи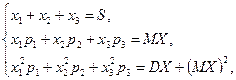 ~
~
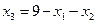 .
. ;
;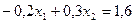 ;
;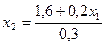 .
.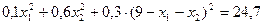 ;
;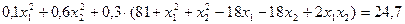 ;
; ;
;
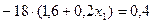 ;
;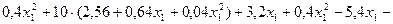
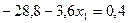 ;
;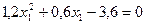 ;
; .
.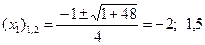 ,
, ,
,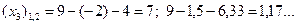
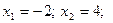
 . Отже, шуканий закон розподілу має вигляд
. Отже, шуканий закон розподілу має вигляд
 (В)
(В) у
у .
. ) = 0,6.
) = 0,6. і щільність (функцію) розподілу, виписати задану і знайдену функцію
і щільність (функцію) розподілу, виписати задану і знайдену функцію 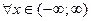 і побудувати їх графіки; б) обчислити числові характеристики
і побудувати їх графіки; б) обчислити числові характеристики 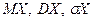 і ймовірність
і ймовірність  .
.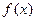 та її область ненульових значень;
та її область ненульових значень;  .
.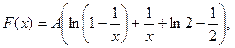


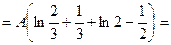
 .
.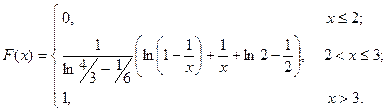 (А)
(А) . Маємо
. Маємо
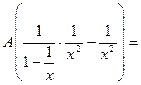

 .
.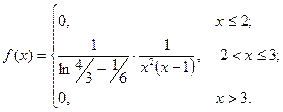 (В)
(В) F(x)
F(x)
 2 y= f (x)
2 y= f (x) ,
,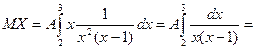
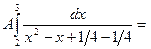


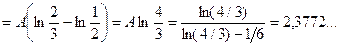 ,
,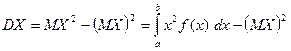 ,
,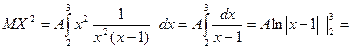
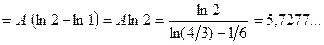 ,
, ,
,
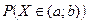 .
.


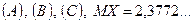 ,
,


 .
.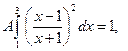

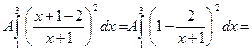

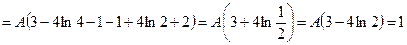 ,
,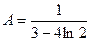 .
. (А)
(А)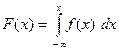 ;
;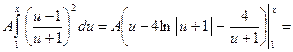
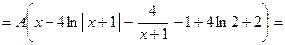
 .
.