Закон Пуассона.
Закон приближения биномиального распределения в случае, когда р – весьма мала, n – весьма велико.
Пусть
(1) Распределение дискретной случайной величины согласно (1) называется распределением Пуассона. Это распределение зависит только от а. Пример. Завод отправил на базу 5000 изделий. Вероятность того, что в пути изделие повредится – 0,0002. найти вероятность того, что на базу прибудут 3 негодных изделия. p =0,0002; k =3; n =5000
§4. Непрерывные случайные величины.
Под непрерывной случайной величиной понимают случайную величину, возможные значения которой сплошь заполняют некоторый промежуток. Определение 1. Пусть F (x) – функция распределения случайной величины Х, F (x) – дифференцируема: Случайная величина Определение 2. Функция
В числителе вероятность того, что случайная величина принимает значение в интервале длиной Δх. Отношение под знаком lim задаёт вероятность, приходящуюся на единицу длины. Беря предел, получим плотность вероятностей. График функции f (x) называется кривой распределения. Заметим, что f (x) существует только для непрерывной случайной величины. Из (*) Отбрасывая бесконечно малую более высокого порядка, получаем приближённое значение.
Из (1) Теорема. Вероятность того, что непрерывная случайная величина принимает значение в интервале от α; до β; Доказательство.
F (x) – первообразная для f (x)
По формуле Ньютона-Лейбница
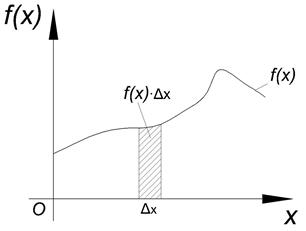
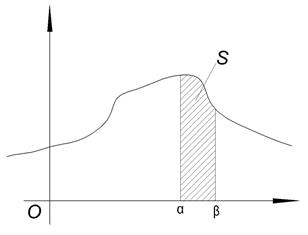
Геометрически:
Свойства f ( x ): 1°. Доказательство: 2°.
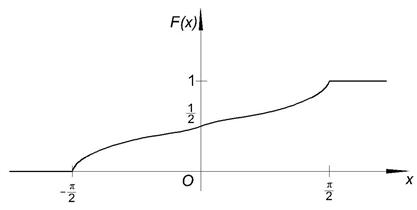
Геометрически 1° и 2° означают, что график функции f (x) расположен выше либо на оси ОХ и площадь под кривой f (x)=1. Пример. Задана функция 1) определить а; 2) построить график f (x); 3) определить F (x) и график; 4) 1) Найдём а:
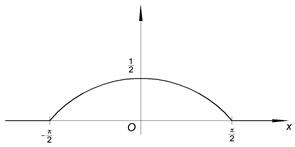
2)
4)
§5. Числовые характеристики случайных величин.
Наиболее полной характеристикой случайной величины является закон её распределения, он даёт все сведения о случайной величине: какие возможные значения она может принимать и с какими вероятностями. Закон распределения случайной величины задаётся функцией распределения F (x) или функцией плотности распределения f (x). На практике часто закон распределения неизвестен, а с другой стороны, нас интересуют более частные сведения, поэтому пользуются более общими характеристиками случайных величин, которые выражают наиболее существенные особенности распределения. Их называют числовыми характеристиками случайной величины: 1) среднее значение или математическое ожидание случайной величины 2) дисперсия случайной величины 3) моменты случайных величин Каждая из этих характеристик с определённой стороны характеризует случайную величину.
|

 (*)
(*) ,
, 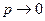 , но
, но 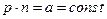 .
.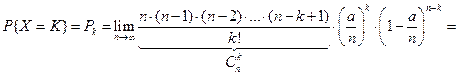

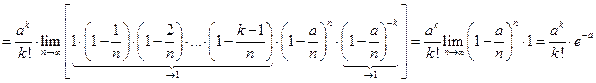
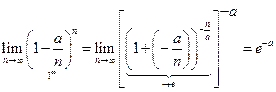
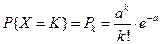 ,
,  .
.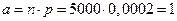
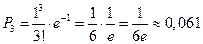 .
. .
.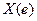 называется непрерывной, если
называется непрерывной, если  неотрицательная функция f (x), интегрируемая на всей числовой оси и такая, что
неотрицательная функция f (x), интегрируемая на всей числовой оси и такая, что 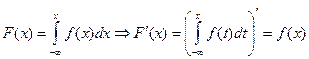 .
.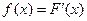 называется плотностью распределения и плотностью вероятностей непрерывной случайной величины.
называется плотностью распределения и плотностью вероятностей непрерывной случайной величины.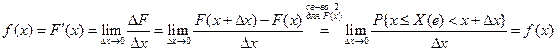 (*)
(*) ;
; 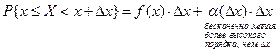
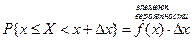
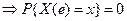 .
.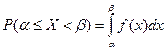 .
.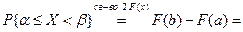
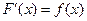
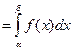 .
.
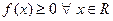
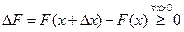 , т.к. по свойству 3 F (x) – неубывающая. Тогда
, т.к. по свойству 3 F (x) – неубывающая. Тогда 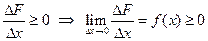 .
.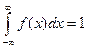
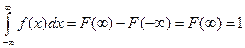
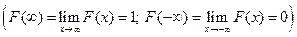
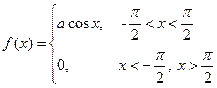
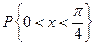 .
.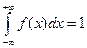
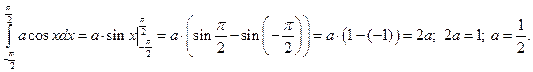
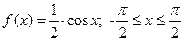
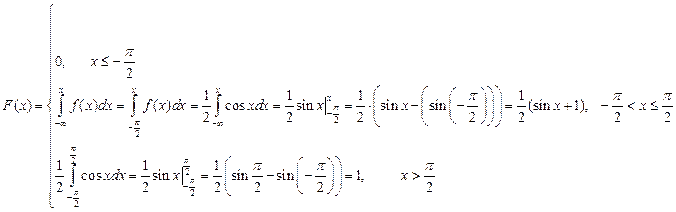 3)
3) 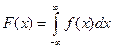
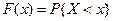
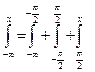
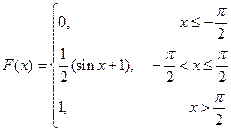
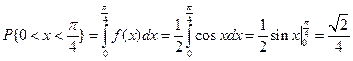 .
.


