Глава 2. Случайные величины.
§1. Определение случайной величины.
Пусть (Е, К, Р) – вероятностная модель некоторого случайного опыта. Рассмотрим примеры числовых функций, аргументом которых является элементарное событие. Пример. 1. Опыт: бросается монета
2. Рассмотрим схему Бернулли с числом испытаний n и вероятностью успеха p.
Каждому элементарному событию e из Е поставим в соответствие число, равное количеству символов У, сколько есть в такой последовательности. Тем самым мы определили числовую функцию 3. На отрезок АВ числовой оси случайным образом бросается точка.
Рассмотрим событие
Случайная величина. Случайная величина и числовая функция элементарного события – это не одно и то же. Мало задать числовую функцию, надо знать вероятности множества значений, которые может принимать эта функция. Определение. Случайной величиной называется числовая функция элементарного события е, определённая на пространстве элементарных событий Е такая, что для любого
Рассмотрим
§2. Функция распределения случайной величины и её свойства.
Определение. Функцию
Эту функцию называют функцией распределения случайной величины Х. Свойства функции распределения случайной величины: 1. 2. Доказательство.
3. F (x) – неубывающая функция,
По свойству 2 4. Если функция F (x) непрерывна при x = x1, то P { X = x1 }=0. Функция y = f (x) непрерывна при x = x1, если Дадим Δx, подсчитаем ΔF: При 5. Укажем без доказательства следующее свойство: 6. 7. F (x) – непрерывна слева:
§3. Дискретные случайные величины.
Случайные величины различны по природе. Нужные в практике удовлетворяют случайные величины дискретные и непрерывные. Случайная величина называется дискретной, если множество её возможных значений является конечным или счётным.
Дискретная случайная величина полностью определена, если заданы вероятности этих возможных значений.
Обычно дискретную случайную величину (закон распределения случайной величины) задают таблицей.
Таблица 1
Эту таблицу называют рядом распределения случайной величины. Пример. Бросаются две игральные кости: зелёная и красная. Рассматривается случайная величина х – сумма выпавших очков на двух костях. Составить закон распределения этой случайной величины.
X = i + j
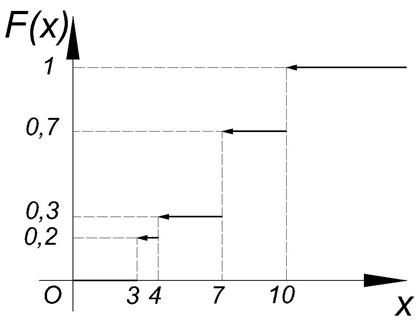
Закон распределения может быть задан функцией распределения дискретной случайной величины. Дискретная случайная величина задана:
Найти функцию распределения и построить её график.
График распределения имеет ступенчатый вид. Скачки происходят в точках, соответствующих возможным значениям и скачки равны вероятности этих значений.
Примеры дискретных распределений случайной величины: 1. В схеме Бернулли с n испытаниями рассмотрим случайную величину X (e)= m – суммарное число успехов за n испытаний. 0, 1, 2, …, n – возможные значения случайной величины.
Распределение X (e) суммарного числа успехов в схеме Бернулли называется биномиальным распределением. Биномиальный ряд распределения случайной величины:
Пример. Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте – 0,1. Составить закон распределения числа отказавших элементов в одном опыте. Случайная величина Х – число отказавших элементов в одном опыте. У – отказ; Р (У)=0,1; q =0,9
|

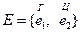
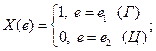
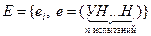
 , m – суммарное число успехов за n испытаний, возможных значений
, m – суммарное число успехов за n испытаний, возможных значений 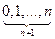 .
.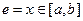
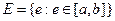
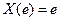 . Возможные значения этой функции сплошь занимают отрезок АВ.
. Возможные значения этой функции сплошь занимают отрезок АВ.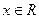 определены вероятности событий
определены вероятности событий 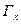 , где
, где 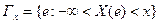 .
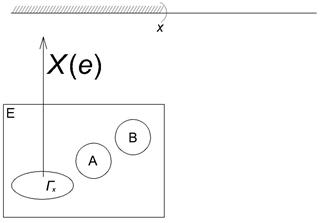
.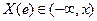 . Числовая функция
. Числовая функция 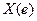 осуществляет отображение пространства Е на числовую ось.
осуществляет отображение пространства Е на числовую ось.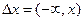
 Требуется, чтобы
Требуется, чтобы 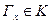 . В противном случае это не будет событием.
. В противном случае это не будет событием.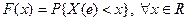 называют функцией распределения.
называют функцией распределения.
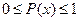 в соответствии с аксиомой 1 и 2.
в соответствии с аксиомой 1 и 2.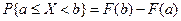
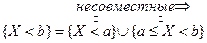

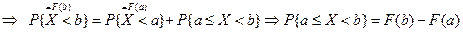 .
.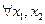 -
- 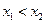
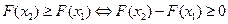
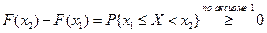 .
.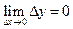 .
.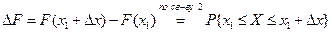
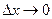 получим
получим 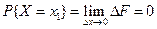 , т.к. F (x) непрерывна при x = x1.
, т.к. F (x) непрерывна при x = x1.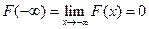 .
.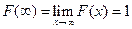 .
.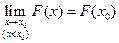 .
.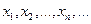
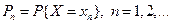 , Pn ≥0
, Pn ≥0
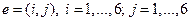
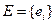 ,
, 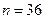 ,
, 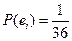
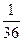
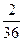
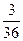

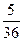
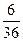
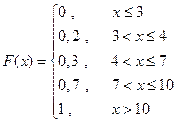
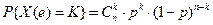
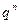
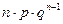
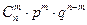

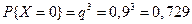 ;
; 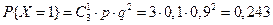 ;
; 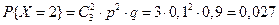 ;
; 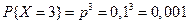 .
.


