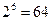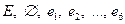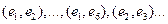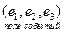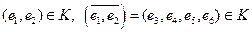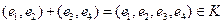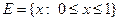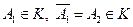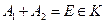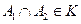Поле событий.
Пусть введено некоторое пространство элементарных событий Е, некоторое подмножество А из Е мы называем событием. Среди множества всех подмножеств пространства Е выделим такой класс К подмножеств пространства, который обладает следующими свойствами: 1) класс К в качестве элементов содержит достоверное и невозможное событие: 2) если 3) если события Такой класс К подмножеств пространства Е называется аддитивным классом. Аддитивный класс К подмножеств А из Е мы будем называть полем событий. Пример. 1) опыт: бросается игральный кубик
В этом случае под событием мы понимаем любое подмножество пространства Е. Поэтому поле событий К в случае дискретного пространства Е есть множество всех подмножеств пространства Е.
Все эти события составляют поле событий. 1. 2. 3. 2) точка случайным образом брошена на отрезок [0;1] и наблюдается 2 события: А1 – попадание точки в промежуток [0;½) A2 – попадание точки в промежуток [½;1]
Под событием понимаем то, что имеет длину. 1. 2.
3.
|
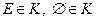
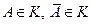
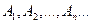(в конечном или счётном числе) принадлежат классу К, то их объединение или пересечение в конечном или счётном числе также принадлежит классу К.
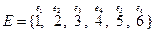- дискретное пространство элементарных событий.
