Глава 1. Случайные события.
§1. Предмет теории вероятностей. Теория вероятностей – это математическая наука, которая изучает закономерности массовых случайных явлений. Все явления реального мира могут быть закономерными и случайными. Закономерное событие – это событие, которое каждый раз осуществляется, как только создаются определённые условия. Случайное явление – такое явление, предсказать исход которого мы не можем. Пример. 1. Отказы технических устройств. Неизвестно, откажет или нет, когда откажет. 2. Промах при серии выстрелов по цели. Промах возникает от того, что не все факторы, от которых зависит данное явление, мы знаем и не все можем учесть. Если фактическое расстояние не совпадает с расчетным, то происходит промах. Форма пули, ствол, метеорологические условия отличаются от расчетных. Однако и в случайных явлениях можно заметить определённые закономерности при их многократном повторении. Пример. 1. Каждая молекула движется хаотично. Масса молекул ведет себя закономерно. 2. При стрельбе по мишени: Ограниченное число выстрелов – нет закономерности в расположении пробоев. Многократное повторение – пробои мишени заполняют эллипс. Чем больше стреляем, тем более отчетливо проявляется закономерность. 3. Проводится опыт, в результате которого может пpоявится событие А, n – количество всех опытов, nA – количество опытов, в результате которых проявилось событие А.
Чем больше количество опытов n, тем отчётливее проявляется закономерность проявления события. Т.е. при многократном проведении опытов частота проявления события стабилизируется около некоторой величины. Такое свойство, характерное для случайных опытов при их многократном проявлении, называется свойством устойчивости частот. Это свойство устойчивости частот при больших n наблюдается и для широкого круга случайных явлений. Случайные явления, которые можно, по крайней мере, принципиально наблюдать много раз, называются массовыми. Факт устойчивости частот, наблюдаемый в массовых случайных явлений, является основой построения теории вероятностей. Однако теория вероятностей имеет дело не со случайными явлениями реального мира, а занимается построением и изучением математических моделей случайных явлений и опытов. Методы теории вероятностей широко используются в различных отраслях науки и инженерной практики: теория надёжности, теория управления, теория стрельбы, теория массового обслуживания, астрономия. Она является теоретической основой для прикладной и математической статистики.
§2. Случайный опыт. Случайные события. Элементарные события.
Будем называть опытом каждое осуществление некоторого комплекса условий и действий, который каждый раз должен строго выполняться при повторении данного опыта. Если результаты опыта неоднозначно определяются условиями опыта и обладают свойством устойчивости частот при его многократном повторении, то такие опыты называются случайными опытами. Всякий факт, который показывает, обладает результат опыта каким-либо свойством или нет, называют случайным событием опыта. Элементарное событие. Элементарным событием случайного опыта будем называть такое событие, которое определяется следующими двумя условиями: 1. В результате опыта происходит одно и только одно элементарное событие e. 2. Каково бы ни было событие А, связанное с данным опытом, после осуществления элементарного события e можно дать однозначный ответ: наступило или нет событие. Любое случайное событие опыта есть некоторая совокупность элементарных событий случайного опыта, характеризуемая каким-либо определённым признаком. Пример. 1. Бросается игральная кость. e – цифра, наблюдаемая на верхней грани кубика. e1 =1, e2 =2, e3 =3, e4 =4, e5 =5, e6 =6. A – выпала четная цифра. А = {2, 4, 6} B – меньше пяти. B = {1, 2, 3, 4} Пример. В ящике 10 шаров, неразличимых на ощупь. Шары помечены номерами 1-10. Шары с номером 1-5 – красные; 6-9 – белые; 10 – синий. Доля шаров красного цвета - Производится опыт: вынимается шар и записывается результат наблюдения: номер шара, его цвет. Затем шар возвращается в ящик и шары в нём перемешиваются. Экспериментатор не знает количество шаров и долю шаров каждого цвета. Поставлена задача: сколь угодно раз повторяя опыт определить количество шаров в ящике и доли шаров каждого цвета. Пусть опыт провели n раз и результаты опыта занесли в таблицу:
Элементарное событие - # шара (1-10). Событие А – красный шар (1,2,3,4,5) Событие В – шар белого цвета (6,7,8,9) Событие С – синий шар (10) Результаты опытов зависят от числа проведённых опытов, т.к. при повторении опытов могут появиться шары с новыми номерами и нового цвета. При увеличении числа опытов n результаты опытов всё меньше и меньше будут пополняться новыми данными о номерах шаров и их цвете, т.е. новыми данными об элементарных событиях и событиях опыта А, В, С. Частоты событий А, В, С будут колебаться незначительно, стабилизируясь около чисел Анализ результатов опыта позволяет ввести математическую модель опыта. Для этого нужно: 1. Задать множество элементарных событий случайного опыта (1, 2, …,10). 2. Составить из данных элементарных событий события случайного опыта А, В, С. 3. Задать на событиях числовую характеристику возможности их появления – вероятности событий. Основанием для введения вероятностей является свойство устойчивости частот.
§3. Пространство элементарных событий.
Для построения математической модели случайного опыта, прежде всего, введём пространство элементарных событий. Множество всех возможных элементарных событий случайного опыта будем называть пространством элементарных событий, связанных с данным случайным опытом Е. В процессе изучения математической модели случайного опыта будем рассматривать только элементы этого множества и его различные подмножества. Пространство элементарных событий называется дискретным, если оно содержит конечное или счётное число элементарных событий. Обозначение для конечного пространства - Е ={ e1, e2,…, en } E = { e1, e2, …, en,…} Любое подмножество А дискретного пространства элементарных событий Е называется событием модели. Говорят, что событие А составлено из элементарных событий или содержит элементарные события. Пример. 1. Бросание кости. E ={ e1, e2, e3, e4, e5, e6 } Любое подмножество этого множества является событием модели. 2. В городе эпидемия гриппа. Случайным образом из населения города отобрали 50 человек, выяснили, сколько из них из них больны гриппом. А – больные гриппом Е – число больных Е ={0, 1, …, 50} A ={0, 1, …,24} В теории вероятностей в качестве пространства элементарных событий используется множество всех точек некоторого промежутка числовой прямой, либо в области на плоскости или области в пространстве. В этом случае пространство элементарных событий называется непрерывным. В случае непрерывного пространства Е под событием понимается не любое подмножество пространства Е, а некоторое подмножество, обладающее определённым свойством. Пример. 1. На плоскость квадрата случайным образом бросается точка. е – точка квадрата, в которой упала брошенная точка. Е – множество всех точек квадрата. Под событием понимается подмножество е, имеющее площадь.
§4. Соотношение между событиями. Действия над событиями.
Задано пространство событий Е А, В, С – события
|

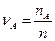 – частота проявления события А в n опытах.
– частота проявления события А в n опытах.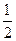 , 6-9 -
, 6-9 - 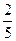 , 10 -
, 10 - 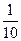 .
.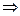 большинство здоровых
большинство здоровых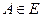 - не является событием.
- не является событием.