Математическое ожидание.
1) Дискретная случайная величина. Пусть дан ряд распределения дискретной случайной величины
Математическим ожиданием дискретной случайной величины называется сумма попарных произведений возможных значений случайной величины на их вероятности.
Выясним вероятностный смысл математического ожидания. Пусть произведено n опытов, в результате которых случайная величина X приняла значения: x1 – m1 раз x2 – m2 раз … xk – mk раз m1 + m2 +…+ mk = n Подсчитаем сумму всех значений, которые случайная величина приняла в n опытах. x1m1 + x2m2 +…+ xkmk – сумма всех значений случайной величины за n опытов. Вычислим среднее значение, которое принимает одна величина.
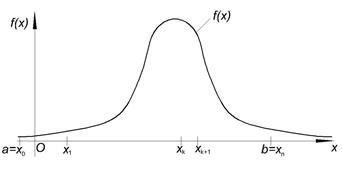
При большом n частоты будут приближаться к соответствующим вероятностям При большом числе опытов среднее значение величины равно значению её математического ожидания. На числовой оси возможные значения случайной величины располагают слева и справа от математического ожидания. Таким образом, математическое ожидание характеризует расположение распределения на числовой оси. 2) Непрерывная случайная величина. Рассмотрим непрерывную случайную величину, у которой известна плотность распределения f (x), и которая принимает возможные значения на [ a, b ].
Рассмотрим разбиение [ a, b ] точками деления x0, x1, x2, …, xk, xk+1, …, xn = b Δxk – длина k -го отрезка разбиения
Если λ; достаточно мало, то приближённо можно считать, что Таким образом, мы фактически можем перейти от непрерывной случайной величины к дискретной случайной величине, которая может принимать возможные значения
Чем меньше λ;, тем точнее математическое ожидание характеризует значение непрерывной случайной величины. Чтобы получить точное равенство, перейдём к причём в правой части равенства предела Так как по определению функция f (x) интегрируема всюду, то предел интегральной суммы существует и равен
Если случайная величина принимает значения на всей числовой оси, то математическое ожидание нужно считать на всей числовой оси.
Определение. Математическим ожиданием непрерывной случайной величины называется интеграл Свойства математического ожидания: 1°. 2°. 3°. 4°.
|

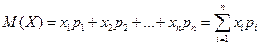
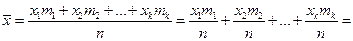
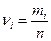 - частота события
- частота события 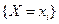
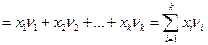
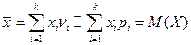 (
(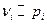 )
)
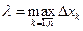 - параметр разбиения
- параметр разбиения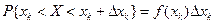
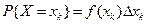 .
.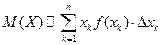
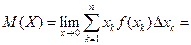
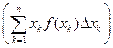 стоит интегральная сумма для
стоит интегральная сумма для 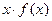 на [ a, b ].
на [ a, b ].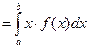 .
.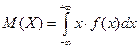
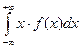 , при этом предполагается, что несобственный интеграл сходится абсолютно, т.е. существует
, при этом предполагается, что несобственный интеграл сходится абсолютно, т.е. существует 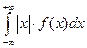 .
.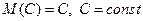 .
.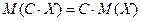 .
.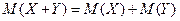 .
.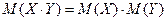 , если X и Y – независимые случайные величины.
, если X и Y – независимые случайные величины.


