Теоремы сложения и умножения вероятностей. Часто используется способ решения той или иной задачи «перебором случаев», когда условия задачи разбиваются на взаимоисключающие друг друга случаи
Часто используется способ решения той или иной задачи «перебором случаев», когда условия задачи разбиваются на взаимоисключающие друг друга случаи, каждый из которых рассматривается отдельно. Например, «направо пойдешь – коня потеряешь, прямо пойдешь – задачу по теории вероятности решать будешь, налево пойдешь –...». Или при построении графика функции у = Пример 7. Из 50 точек 17 закрашены в синий цвет, а 13 – в оранжевый цвет. Найти вероятность того, что случайным образом выбранная точка окажется закрашенной. Решение. Всего закрашено 30 точек из 50. Значит, вероятность равна Ответ: 0,6.
Обозначим буквой С интересующее нас событие. Событие С наступает тогда и только тогда, когда происходит хотя бы. одно из событий А или В. Ясно, что N(С) = N(А) + N(В). Поделим обе части этого равенства на N – число всех возможных исходов данного опыта; получим Мы на простом примере разобрали важную и часто встречающуюся ситуацию. Для нее есть специальное название. Определение 2. События А и В называют несовместными,если они не могут происходить одновременно. В противном случае события называются совместными.
|

 рассматривают случаи х < -1;
рассматривают случаи х < -1; 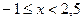 ;
;  . В каждом из трех случаев «раскрывают» модуль, строят нужные графики линейных функций и затем объединяют соответствующие части этих графиков; фактически речь идет о построении графика кусочной функции. Этот же метод часто используют и при подсчете вероятностей.
. В каждом из трех случаев «раскрывают» модуль, строят нужные графики линейных функций и затем объединяют соответствующие части этих графиков; фактически речь идет о построении графика кусочной функции. Этот же метод часто используют и при подсчете вероятностей.
 Рассмотрим, однако, этот простой пример более внимательно. Пусть событие А состоит в том, что выбранная точка – синяя, а событие В состоит в том, что выбранная точка – оранжевая (рисунок). По условию, события А и В не могут произойти одновременно.
Рассмотрим, однако, этот простой пример более внимательно. Пусть событие А состоит в том, что выбранная точка – синяя, а событие В состоит в том, что выбранная точка – оранжевая (рисунок). По условию, события А и В не могут произойти одновременно. .
.


