Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность произведения этих событий.Р(А+В)=Р(А)+Р(В)-Р(АВ) Пусть А и В – два случайных события одного и того же испытания. Тогда условной вероятностью события А или вероятностью события А при условии, что наступило событие В, называется число Из этого определения следует, что Р(АВ)=Р(В)Р(А/В), т.е. вероятность произведения двух совместных событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло. Пример 10. Из колоды в 36 карт поочередно достают две карты. Найти вероятность того, что вторым вынут червовый король, если первая карта – король черной масти. Решение. Событие А состоит в одновременном наступлении двух совместных событий: А2 – вынут король червей и А1 – вынут король черной масти. При этом наступление события А2 зависит от наступления события А1. Найдем вероятности каждого из событий А1 и А2.
Теперь найдем вероятность события А: Событие А называется независимым от события В, если наступление события В не влияет на вероятность наступления события А.
|
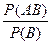(при этом В¹V). Обозначают Р(А/В).
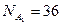(т.к. в колоде всего 36 карт и мы берем 1 карту). N(A1) = 2 (т.к. в колоде 2 короля черной масти). Тогда 
.
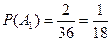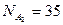(т.к. мы одну карту из колоды вынули). N(A2) = 1 (т.к. в колоде 1 король червей и мы вынули не его). Тогда 
.
.
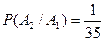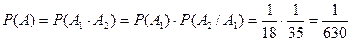