ТЕОРЕМА 3: (теорема умножения вероятностей). Вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий.
Р(АВ)=Р(В)Р(А) События А1, А2, …, Ап называются независимыми, если любые два из них попарно независимы и выполняется равенство Р(А1А2…Ап)= Р(А1)Р(А2)…Р(Ап). Пример 11. В первой урне находятся 6 черных и 4 белых шара, во второй – 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми? Решение. Пусть А1 – из первой урны извлечен белый шар; А2 – из второй урны также извлечен белый шар. Очевидно, что события А1 и А2 – независимы. Р(А1) = По теореме: Р(А1А2) = Пример 12. В экзаменационные билеты включено по два теоретических вопроса и по одной задаче. Всего составлено 28 билетов. Вычислить вероятность того, что, вынув наудачу билет, студент ответит на все вопросы, если он подготовил 50 теоретических вопросов и 22 задачи. Решение. Полный ответ на билет состоит из произведения двух событий: студент одновременно ответит на два вопроса (событие А) и решит задачу (событие В). Число всех возможных комбинаций из 56 вопросов по два составляет Так как студент подготовил только 50 вопросов, то число благоприятных исходов равно
Вероятность события В определяется тем, что студент знает 22 задачи из 28 возможных Р(В) = Р(АВ)=Р(А)Р(В) = В заключение обсудим следующий принципиальный вопрос: можно ли доказать, что вероятность выпадения «решки» при одном бросании монеты равна –. Ответ отрицательный. Вообще говоря, сам вопрос не корректен, неясен точный смысл слова «доказать». Ведь доказываем мы что-либо всегда в рамках некоторой модели, в которой уже известны правила, законы, аксиомы, формулы, теоремы и т. п. Если речь идет о воображаемой, «идеальной» монете, то потому-то она и считается идеальной, что, по определению, вероятность выпадения «решки» равна вероятности выпадения «орла». А, в принципе, можно рассмотреть модель, в которой вероятность выпадения «решки» в два раза больше вероятности выпадения «орла» или в три раза меньше и т. п. Тогда возникает вопрос: по какой причине из различных возможных моделей бросания монеты мы выбираем ту, в которой оба исхода бросания равновероятны между собой? Совсем лобовой ответ таков: «А нам так проще, понятнее и естественнее!» Но есть и более содержательные аргументы. Они приходят из практики. В подавляющем большинстве учебников по теории вероятностей приводят примеры французского естествоиспытателя Ж. Бюффона (XVIII в.) и английского математика-статистика К. Пирсона (конец XIX в.), которые бросали монету, соответственно, 4040 и 24000 раз и подсчитывали число выпадений «орла» или «решки». У них «решка» выпала, соответственно, 1992 и 11988 раз. Если посчитать частоту выпадения «решки», то получится Кстати, вы вполне можете проверить это предположение даже на большем числе бросаний монеты. Например, если за один день каждый из 25 студентов вашей группы 40 раз бросит монету, то уже получится 1000 бросаний. За месяц «набежит» очень большое число. Подведем итоги. Основное понятие – вероятность случайного события, подсчет которой производится в рамках простейшей модели – классической вероятностной схемы. Важное значение и в теории, и в практике имеет понятие противоположного события и формула Р( Наконец, мы познакомились с несовместными событиями и с формулами Р(А + В) = Р(А) + Р(В), Р(А + В + С) = Р(А) + Р(В) + Р(С), позволяющими находить вероятности суммы таких событий.
Контрольные вопросы: 1.Что называется испытанием? 2.Как называется результат испытания? 3.Какие виды событий бывают, чем они отличаются? 4.Что такое статистическая вероятность события? 5.Опишите классическую схему нахождения вероятности события. 6.Сформулируйте определение классической вероятности события. 7.Какие события называются противоположными? 8.Чему равна вероятность достоверного события, невозможного события? 9.Какие события называют несовместными? 10. Как можно найти вероятность одного из двух противоположных событий? 11. Какие события называются независимыми? 12. Сформулируйте теоремы сложения и умножения вероятностей.
|

 , Р(А2) =
, Р(А2) = 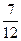 .
.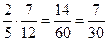 .
. .
. . Р(А)=
. Р(А)= 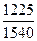 .
.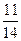 .
.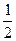 .
. у Бюффона и
у Бюффона и  у Пирсона. Возникает естественное предположение, что при неограниченном увеличении числа бросаний монеты частота выпадения «решки», как и частота выпадения «орла», все больше и больше будет приближаться к 0,5. Именно это предположение, основанное на практических данных, является основой нашего выбора в пользу модели с равновероятными исходами.
у Пирсона. Возникает естественное предположение, что при неограниченном увеличении числа бросаний монеты частота выпадения «решки», как и частота выпадения «орла», все больше и больше будет приближаться к 0,5. Именно это предположение, основанное на практических данных, является основой нашего выбора в пользу модели с равновероятными исходами.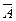 ) = 1 - Р(А) для нахождения вероятности такого события.
) = 1 - Р(А) для нахождения вероятности такого события.


