Лекция 21. Взаимодействие γ-квантов с веществом
21.1. Общие замечания. Процесс взаимодействия фотонного излучения с веществом с передачей ему энергии нельзя считать непрерывным, как это имеет место в случае тяжелых заряженных частиц. При прохождении через вещество фотон в единичном акте электромагнитного взаимодействия с атомом теряет всю свою энергию (поглощение) или значительную ее часть (рассеяние); в последнем случае фотон существенно изменяет и направление своего движения. Поэтому, в отличие от заряженных частиц, для фотонов не существует понятия пробега или потерь энергии на единицу длины пути. Известно множество различных видов взаимодействия электромагнитного излучения с атомами. Однако, если только не считать ядерных реакций, уже рассматривавшихся в п. 17.4, основными видами взаимодействия с веществом для фотонов высокой энергии (вне зависимости от происхождения: γ-кванты, рентгеновское излучение и т.п.) являются фотоэффект, эффект Комптона и образование электрон-позитронных пар. 21.2. Фотоэффект. Фотоэффект, или фотоэлектрическое поглощение – это вырывание связанных атомных электронов под действием электромагнитного излучения.[176] Энергия γ-кванта Еg передается электрону, который переходит из связанного состояния в свободное: g + А ® А + + e -. Фотоэффект невозможен на свободных (не связанных) электронах, так как для выполнения закона сохранения импульса, кроме фотона и электрона, необходимо присутствие третьего тела – атомного ядра (ПРИЛОЖЕНИЕ К). Вероятность фотоэффекта тем больше, чем ближе энергия падающего кванта к энергии связи электрона. Поэтому фотоэлектрическое поглощение γ-квантов чаще всего происходит при взаимодействии с электроном одной из внутренних оболочек атома. С точностью до энергии отдачи иона А +, которая мала даже в случае легких атомов, кинетическая энергия фотоэлектрона определяется как
где Ii – энергия связи электрона на i -й атомной оболочке. Очевидно, что при Еg < Ii фотоэффект невозможен. Освободившееся на электронной оболочке место заполняется одним из электронов с вышерасположенных оболочек. Этот процесс сопровождается испусканием характеристического рентгеновского излучения и электронов Оже, возникающих при разрядке возбужденных состояний атома (последнее с большей вероятностью наблюдается при фотоэффекте на атомах с малыми и средними значениями атомного номера Z). Ввиду того, что масса ядра значительно больше массы электрона, бóльшая часть импульса γ-кванта передается ядру. Вероятность передачи импульса электрону зависит от энергии связи электрона с ядром и энергии γ-кванта. Именно этими обстоятельствами и обусловлены основные характеристики фотоэффекта в области высоких энергий: 1) зависимость сечения от энергии; 2) зависимость сечения от заряда ядра вещества-поглотителя; 3) соотношение вероятностей фотоэффекта на разных электронных оболочках. Формулы для сечения фотоэффекта были получены методами квантовой электродинамики. Сечение фотоэффекта для атома водорода или для легкого водородоподобного иона с зарядом ядра Z определяется следующим выражением:
где a – постоянная тонкой структуры, re – классический радиус электрона,
(βe – скорость фотоэлектрона в единицах c). Можно заметить, что вероятность фотоэффекта сильно зависит от заряда ядра (~ Z 5), так как с ростом Z резко увеличивается энергия связи внутренних электронов с ядром (кулоновское взаимодействие). В нерелятивистском случае, когда Ii << Еg << mec 2
В ультрарелятивистском случае, когда
Полное сечение фотоэффекта для многоэлектронных атомов может быть вычислено только приблизительно с использованием численных методов. Однако при этом пропорциональность σФ ~ Z 5 и асимптотики σФ (Еg) в пределе малых и больших энергий фотона остаются справедливыми. Если проследить, как выглядит зависимость сечения фотоэффекта на многоэлектронном атоме по мере увеличения Еg, то можно видеть две основные особенности: наличие резких краев поглощения на пороге ионизации Ii каждой оболочки и очень быстрый спад сечения по мере увеличения энергии после каждого из значений Еg = Ii (рис. 21.1). Сочетание этих двух особенностей создает характерную пилообразную форму зависимости сечения от энергии. Вероятность фотоэффекта на L -, M - и других оболочках значительно меньше, чем на К -оболочке: при энергиях γ-квантов, превышающих энергию связи на K -оболочке, sL/sK ≈ 1/5, sM/sL ≈ 1/4. Вероятность фотоэффекта на внешних оболочках крайне мала. 21.3. Эффект Комптона. При прохождении g-квантов через вещество, наряду с поглощением, происходит их рассеяние с изменением или же без видимого изменения длины волны. Рассеяние без изменения длины волны характерно для сравнительно мягкого рентгеновского излучения (Еg << mec 2). Оно называется классическим, или томсоновским и находит свое объяснение в рамках классической электродинамики: падающая на атом электромагнитная волна приводит в вынужденные колебания связанные электроны, которые сами становятся излучателями волн с той же частотой (длиной волны). Для сечения классического рассеяния Дж. Дж. Томсон получил следующую формулу:
Рассеяние с изменением длины волны имеет место в тех случаях, когда энергия фотона сравнима с mec 2. Впервые это явление наблюдал А. Комптон (1922 г.) при исследовании рассеяния жестких рентгеновских лучей. В опытах Комптона было показано, что спектр рассеянного излучения, помимо первоначальной линии с длиной волны Полное сечение, определяющее число g-квантов, выбывших из первичного пучка (в расчете на один электрон), дается формулой Клейна-Нишины-Тамма:
где x = 2 Eγ / mec 2. Рассмотрим ее предельные случаи. При x << 1 (нерелятивистский случай) число рассеянных g-квантов линейно убывает с ростом энергии g-квантов
В обратном, ультрарелятивистском случае (x >> 1)
Таким образом, сечение комптоновского рассеяния уменьшается с ростом энергии фотона; в пределе Eg ® ¥ практически обратно пропорционально Eg (рис. 21.1). Полное сечение рассеяния γ-квантов на атоме пропорционально числу электронов, т.е. Энергетический спектр электронов отдачи (комптоновских электронов) непрерывен: их кинетическая энергия Te распределена в интервале от 0 до максимальной величины, определяемой формулой Л.8 (ПРИЛОЖЕНИЕ Л). Указанный на рис. 21.1 ход кривой, изображающей зависимость sК от Еg, относится к случаю бесконечно узкого пучка и точечного детектора, когда рассеянные на небольшой угол g-кванты не регистрируются. Однако на опыте употребляются пучки с конечным углом раствора, а детектор не является точечным. Поэтому весьма важно знание углового распределения рассеянных g-квантов.
В некоторых случаях необходимо учитывать скорости электронов, взаимодействующих с фотонами. Движение атомных электронов приводит к заметному разбросу энергий рассеянных фотонов и электронов отдачи (при фиксированном θ;). В частности, если импульс электрона больше импульса летящего ему навстречу фотона, то последний не теряет, а приобретает энергию (обратный эффект Комптона). Кроме электронов эффект Комптона может происходить и на других заряженных (а также нейтральных, но имеющих ненулевой магнитный момент) частицах, например на протоне или нейтроне. Однако сечения рассеяния при этом очень малы, так как обратно пропорциональны квадрату массы частицы. В заключение обсуждения комптоновского рассеяния g-квантов отметим, что с этим явлением связано не только их рассеяние, но и последующее фотоэлектрическое поглощение в веществе. Если источник g-квантов со всех сторон окружить достаточно большими блоками из легкого вещества (например, алюминия), то за пределы блоков g-излучение уже не выйдет. Это будет не так, если бы имело место классическое рассеяние. Однако при комптоновском рассеянии часть энергии g-кванта передается электрону. Поэтому в результате многократного рассеяния в блоке g-квант постепенно потеряет большую часть своей энергии, и, в конце концов, поглотится, так как сечение фотоэффекта быстро растет с уменьшением энергии и становится больше, чем сечение рассеяния (рис. 21.1). На явлении многократного рассеяния основано устройство защиты от g-квантов из бетона, кирпича и т.д. 21.4. Образование электрон-позитронных пар. При энергиях g-квантов, превышающих 2 mec 2 (1,022 МэВ), наблюдается процесс поглощения g-квантов с образованием пары электрон-позитрон: g + а ® e – + e + + а. Энергия g-кванта тратится на создание этих двух частиц и на сообщение им кинетической энергии; таким образом, образование пары – эндотермический процесс. Исходя из законов сохранения энергии и импульса, можно показать, что образование пары в вакууме невозможно (ПРИЛОЖЕНИЕ К). Это может происходить только при взаимодействии g-излучения с другими частицами. В результате образования пары энергия и импульс должны распределиться между электроном, позитроном и какой-то третьей частицей (ядром или электроном), в поле которой образовалась пара. Если применить к процессу образования пары анализ, изложенный в п. 11.2, станет ясно, что при образовании пары в поле ядра пороговая энергия фотона равна 2 mec 2, а в поле электрона 4 mec 2.[178] Оценим энергию отдачи при рождении пары в поле ядра. Максимальная отдача будет наблюдаться в том случае, если электрон и позитрон вылетают под углами 90о относительно направления движения γ-кванта, причем угол их разлета равен 180о. В этом случае импульс ядра отдачи равен импульсу γ-кванта, и для энергии отдачи справедлива формула (9.6). Отсюда получаем, что для Еg = 10 МэВ при атомной массе вещества А > 10 энергия ядер отдачи не превышает 5 кэВ (т.е. менее 0,05%). Тогда сумма кинетических энергий электрона и позитрона с хорошей точностью равна
При относительно малых величинах Еg эта энергия распределяется почти равновероятно между электроном и позитроном. С ростом Еg преобладающим становится асимметричное распределение. Спектры электронов и позитронов несколько различаются, если принять во внимание, что при удалении от ядра, в поле которого образовалась пара, электроны испытывают торможение, а позитроны ускорение. Этот эффект тем больше, чем выше заряд ядра Z и чем меньше Еg. Испускание электрона и позитрона при больших энергиях γ-кванта происходит в направлении движения последнего в пределах угла θ; ≈ mec 2/ Еg. При малых энергиях угловое распределение менее анизотропно и зависит от Z. Чем сильнее электрическое поле частицы, с которой взаимодействует γ-квант, тем вероятнее образование пар. Для сечения образования пары в поле «голого» ядра квантовая электродинамика дает следующее выражение:
Для легких атомов (aZ << 1) σП ~ Z 2. Учет экранирования ядра атомными электронами приводит к тому, что в пределе Eg ® ¥ сечение процесса практически перестает зависеть от Eg. Энергетическая зависимость сечения образования пар показана на рис. 21.1. При малых энергиях и больших Z сечение образования пары в поле электрона примерно в 103 раз меньше. Однако при Еg > 10 МэВ оно составляет около 1% общего сечения в тяжелых элементах и около 10% в легких. Энергия отдачи, получаемая атомным электроном, в этом случае того же порядка, что и кинетическая энергия частиц пары. Образование электрон-позитронных пар в сочетании с радиационным торможением является причиной возникновения электрон-фотонных ливней в космических лучах (п. 18.6). Если фотон тормозного излучения имеет энергию Еg >> mec 2, он может образовать пару, электрон и позитрон которой при торможении снова создают фотоны, и т.д. Процесс нарастает лавинообразно до тех пор, пока не будет достигнута критическая энергия (п. 20.4). В широком диапазоне энергий γ-квантов суммарное сечение их взаимодействия с веществом s Σ складывается из сечений трех основных процессов – фотоэффекта, эффекта Комптона и образования пар:
Из характера зависимости каждого из этих сечений от энергии γ-квантов следует, что в области малых энергий основным механизмом взаимодействия является фотоэффект, в промежуточной области – эффект Комптона,[179] а в области высоких энергий – образование электрон-позитронных пар. Значения энергии, отделяющие области преобладания каждого из трех эффектов, различны для разных сред. Сечение σ;Σ имеет минимум в области, где наиболее велико влияние комптоновского рассеяния (рис. 21.1). Этот минимум особенно резко выражен для тяжелых элементов. 21.5. Коэффициент ослабления. Экспоненциальный закон поглощения γ-квантов. Итак, при прохождении через вещество g-излучение в общем случае испытывает поглощение и рассеяние. Как при поглощении, так и при рассеянии g-квант выбывает из падающего пучка в результате единичного акта. Число g-квантов, удаляемых из пучка при прохождении поглотителя толщиной dx, пропорционально dx и числу g-квантов N, падающих на слой dx. Таким образом, уменьшение числа g-квантов в пучке равно
Коэффициент пропорциональности m называется полным линейным коэффициентом ослабления. Как следует из (21.9), линейный коэффициент ослабления имеет физический смысл относительного уменьшения числа g-квантов в пучке, приходящееся на единицу длины пути в веществе. Очевидно, величине m можно придать и другой смысл: это среднее число столкновений g-кванта с атомами на единице пути, если в результате такого столкновения g-квант выбывает из пучка. Отсюда величину 1/ m можно истолковать как среднюю длину свободного пробега g-кванта в веществе: Rγ = 1/ μ;. Ослабление пучка в слое вещества вследствие каждого из трех процессов, рассматривавшихся выше, происходит, очевидно, независимо. Следовательно, полный коэффициент ослабления равен
где t и χ; – коэффициенты поглощения, отвечающие фотоэффекту и образованию пар, ξ; – коэффициент ослабления при эффекте Комптона, n 0 – число атомов в единице объема вещества. Линейный коэффициент ослабления за счет комптоновского рассеяния выражается также формулой
где NA – число Авогадро; r – плотность поглотителя; А – его атомная масса.
– универсальную величину, зависящую только от энергии g-кванта и поэтому пригодную для любого поглотителя. Пусть имеется источник монохроматических g-квантов и их поглотитель (рис. 21.3). Используя детектор γ-излучения малых размеров и выбрав большое расстояние между источником и детектором, выделим узкий, почти параллельный пучок γ-квантов. Выберем диаметр поглотителя, равный диаметру пучка d. Можно сделать так, чтобы величина d была много меньше длины свободного пробега g-квантов в поглотителе по отношению к комптоновскому рассеянию. Тогда однажды рассеянный квант не возвратится в пучок и не попадет в детектор. Следовательно, коэффициент ослабления не будет зависеть от толщины поглотителя, и можно проинтегрировать (21.9) по x:
Выражение (21.12) называется экспоненциальным законом поглощения γ-квантов. Оно справедливо в условиях т.н. хорошей геометрии опыта, когда исследуется прохождение узкого параллельного пучка γ-лучей: в этом случае не только фотоэффект и образование пар, но и комптоновское рассеяние выводит γ-кванты из пучка. Если спектр γ-излучения содержит несколько линий, то N = N 1 + N 2 + ···, и уравнение (21.9) должно быть заменено системой уравнений. Так как каждая компонента g-излучения поглощается независимо, то для каждой из них справедлива формула (21.12). Отсюда интенсивность пучка после прохождения поглотителя, имеющего толщину x, будет равна
В случае плохой геометрии (широкий пучок или пучок, имеющий большой угол раствора) рассеянные γ-кванты, остаются в пучке, и закон поглощения, строго говоря, уже нельзя выразить уравнением (21.9), так как в пучке будут встречаться многократно рассеянные g-кванты, имеющие меньшую энергию, чем падающие, и, соответственно, характеризуемые другим значением m. Уравнение (21.12) работает, однако, и в этом случае лучше, чем можно было ожидать. Причина хорошего согласия заключается в том, что γ-кванты с энергией 1-2 МэВ, потерявшие энергию из-за комптоновского рассеяния, быстро выбывают из пучка из-за резкого увеличения сечения фотоэффекта. Поэтому при использовании не слишком широких пучков удается ввести некоторое среднее или эффективное значение μ;. Однако оно отличается от теоретического и зависит от геометрии опыта. Строгое вычисление ослабления интенсивности широкого пучка g-лучей при прохождении больших блоков вещества представляет собой достаточно сложную математическую задачу. Ослабление широкого или расходящегося пучка монохроматических γ-квантов часто представляют в виде
где величина B (Еg, Z, μx) называется фактором накопления. Фактор накопления показывает, во сколько раз увеличивается интенсивность широкого пучка за слоем поглотителя в сравнении с интенсивностью узкого пучка в той же точке. Значения B (Еg, Z, μx) табулированы для различных вариантов геометрии источника и поглотителя.
|

 , (21.1)
, (21.1)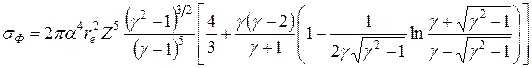 ,
,
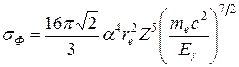 . (21.2)
. (21.2)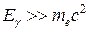 ,
,

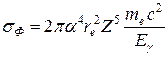 . (21.3)
. (21.3)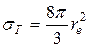 . (21.4)
. (21.4)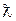 , содержит смещенную линию
, содержит смещенную линию 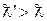 , причем величина смещения
, причем величина смещения 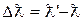 растет с увеличением угла рассеяния θ;, а при фиксированном θ; не зависит ни от
растет с увеличением угла рассеяния θ;, а при фиксированном θ; не зависит ни от 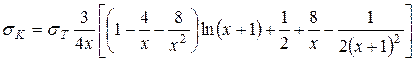 , (21.5)
, (21.5)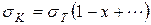 .
.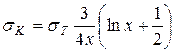 .
.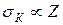 .
. При малых значениях x угловое распределение следует закону (1 + cos2 φ;), характерному для классической электромагнитной теории (φ – угол рассеяния γ-кванта). Это распределение симметрично относительно φ = π/2. Вероятность рассеяния максимальна при φ; = 0о и 180о. С увеличением x угловое распределение становится все более и более направленным вперед. Кривые рис. 21.2 иллюстрируют характер углового распределения рассеянного g-излучения для различных значений Еg. При x >> 1 практически все рассеянное излучение можно считать сосредоточенным в узком конусе с углом раствора φ; = 2/ x.
При малых значениях x угловое распределение следует закону (1 + cos2 φ;), характерному для классической электромагнитной теории (φ – угол рассеяния γ-кванта). Это распределение симметрично относительно φ = π/2. Вероятность рассеяния максимальна при φ; = 0о и 180о. С увеличением x угловое распределение становится все более и более направленным вперед. Кривые рис. 21.2 иллюстрируют характер углового распределения рассеянного g-излучения для различных значений Еg. При x >> 1 практически все рассеянное излучение можно считать сосредоточенным в узком конусе с углом раствора φ; = 2/ x.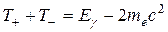 . (21.6)
. (21.6)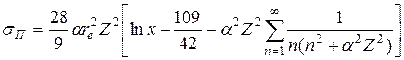 . (21.7)
. (21.7) . (21.8)
. (21.8) . (21.9)
. (21.9)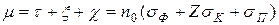 , (21.10)
, (21.10) ,
, Ввиду того, что Z/A мало изменяется при переходе от вещества к веществу (от 0,5 до 0,4 в пределах периодической таблицы), линейный коэффициент ослабления за счет комптоновского рассеяния зависит практически только от плотности вещества. Если поглотитель состоит из элементов с малыми Z, ослабление пучка g-квантов определяется, в основном, эффектом Комптона (при средних значениях Еg). В этом случае, ввиду того, что ξ; пропорционален плотности r, а отношение Z/A приблизительно постоянно, можно ввести массовый коэффициент ослабления
Ввиду того, что Z/A мало изменяется при переходе от вещества к веществу (от 0,5 до 0,4 в пределах периодической таблицы), линейный коэффициент ослабления за счет комптоновского рассеяния зависит практически только от плотности вещества. Если поглотитель состоит из элементов с малыми Z, ослабление пучка g-квантов определяется, в основном, эффектом Комптона (при средних значениях Еg). В этом случае, ввиду того, что ξ; пропорционален плотности r, а отношение Z/A приблизительно постоянно, можно ввести массовый коэффициент ослабления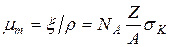 (21.11)
(21.11)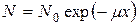 . (21.12)
. (21.12) . (21.13)
. (21.13) , (21.14)
, (21.14)


