Регрессионный анализ
Регрессионный анализ — метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионный анализ — это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами. Взаимосвязь между средним значением результирующей переменной и средними значениями предикторов выражается в виде уравнения регрессии. Уравнение регрессии – математическая функция, которая подбирается на основе исходных статистических данных зависимой и объясняющих переменных. Чаще всего используется линейная функция. В этом случае говорят о линейном регрессионном анализе. Регрессионный анализ очень тесно связан с корреляционным анализом. В корреляционном анализе исследуется направление и теснота связи между количественными переменными. В регрессионном анализе исследуется форма зависимости между количественными переменными. Т.е. фактически оба метода изучают одну и ту же взаимосвязь, но с разных сторон, и дополняют друг друга. На практике корреляционный анализ выполняется перед регрессионным анализом. После доказательства наличия взаимосвязи методом корреляционного анализа можно выразить форму этой связи с помощью регрессионного анализа. Цель регрессионного анализа – с помощью уравнения регрессии предсказать ожидаемое среднее значение результирующей переменной. Основные задачи регрессионного анализа следующие: ü определения вида и формы зависимости; ü оценка параметров уравнения регрессии; ü проверка значимости уравнения регрессии; ü проверка значимости отдельных коэффициентов уравнения; ü построение интервальных оценок коэффициентов; ü исследование характеристик точности модели; ü построение точечных и интервальных прогнозов результирующей переменной. Из корреляционного анализа были выбраны влияющие переменные: y1 = f (x2; x4; x8); y3 = f (x4; x5; x8). Регрессионный анализ для у1:
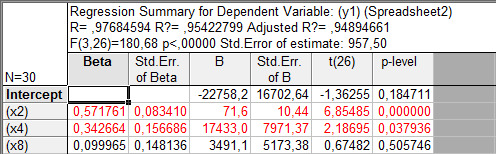
Рис. 15 Статистические показатели регрессии
Рис. 16 Количественное значение показателей регрессионной зависимости N - объем изучаемой совокупности; R - теоретическое корреляционное отношение;
Adjusted F (3; 26) - расчетное значение критерия Фишера (в скобках приведено число степеней свободы факторной и остаточной дисперсий); p - уровень значимости; Std.Err.of Estimate - стандартная ошибка уравнения.
у1 = -22758,2 + 71,6*х2 + 17433*х4 +3491,1*х8 R2=0, 97684594
Регрессионный анализ для у3:
Рис. 17 Статистические показатели регрессии
Рис. 18 Количественное значение показателей регрессионной зависимости N - объем изучаемой совокупности; R - теоретическое корреляционное отношение;
Adjusted F (3;26) - расчетное значение критерия Фишера (в скобках приведено число степеней свободы факторной и остаточной дисперсий); p - уровень значимости; Std.Err.of Estimate - стандартная ошибка уравнения.
У3 = -8,72643 + 0,05292*х2 + 13,33768*х4 +1,03727*х8; R2=0, 998049499
|


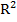 - коэффициент детерминации;
- коэффициент детерминации;




