Нахождение трендов показателей
Одной из важных целей анализа при исследовании любого экономического процесса является обеспечение возможности его прогнозирования на перспективу. Этой цели зачастую служат инструменты регрессионного анализа, которые позволяют строить уравнения тренда по исходному временному ряду. Чем длиннее временной ряд, тем точнее будет уравнение, полученное по нему и, соответственно, тем достовернее будет полученный прогноз. Однако, это не всегда справедливо: если ряд развивается волнообразно, с разнонаправленными тенденциями на разных временных отрезках, если имеют место резкие скачки как в положительную, так и в отрицательную стороны, то следует с осторожностью относиться к такому ряду и проводить тщательный предварительный анализ, который должен заключаться в разделении временного ряда на определенные интервалы, для которых характерна схожая тенденция, поскольку без этого полученное уравнение тренда не будет с достаточной точностью аппроксимировать имеющиеся данные и не обеспечит необходимую точность прогнозных показателей на перспективу. Как показал предварительный анализ, практически ни одно из изучаемых явлений не развивается по прямолинейной закономерности, и даже отдаленно не напоминает прямую линию. За период с 1970 по 2014 гг. в экономике многих стран происходили значительные изменения, вызванные как внутренними причинами, так и причинами внешнеэкономического характера. Все это приводило в отдельные годы к «пикам» и «ямам» в развитии, образовывало «белый шум», который, если не принимать во внимание его нетипичность в основной тенденции, будет значительно снижать точность полученного по таким рядам уравнения тренда. Поскольку по условиям задачи необходимо рассчитать уравнение тренда по заранее известной модели – уравнению прямой, - можно сразу сказать с уверенностью, что полученные данные не будут обладать достаточной точностью и могут лишь примерно описать основную тенденцию в развитии анализируемых явлений. Все расчеты уравнений тренда были произведены с использованием средств MSExcel, позволяющего строить тренд к временному ряду. Тренды описываются уравнениями:
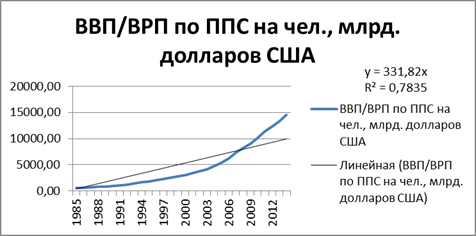
Рис.1 Тренд показателя ВВП по ППС на душу населения, млрд. долларов США
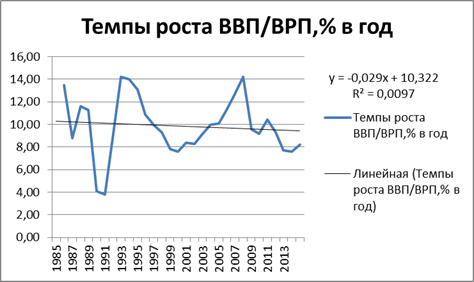
Рис. 2 Тренд показателя роста ВВП по ППС
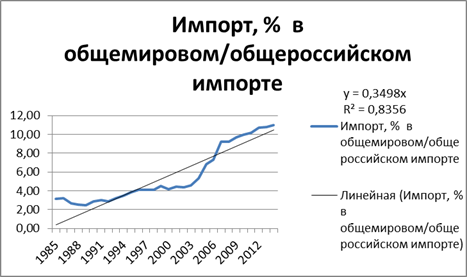
Рис. 3 Тренд показателя доли импорта в общемировом импорте
Рис. 4 Тренд показателя доли импорта hi-tech в общем импорте
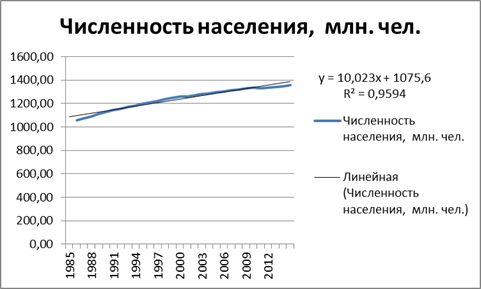
Рис. 5 Тренд показателя численности населения
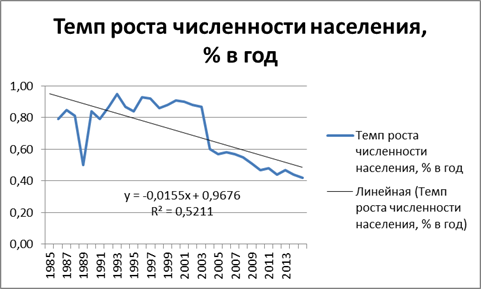
Рис. 6 Тренд показателя роста численности населения
Рис. 7 Тренд показателя стоимости нефти на мировом рынке
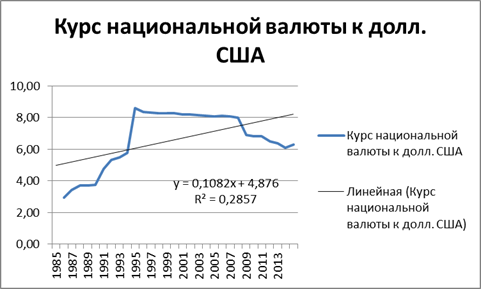
Рис. 8 Тренд показателя курса национальной валюты к долл. США
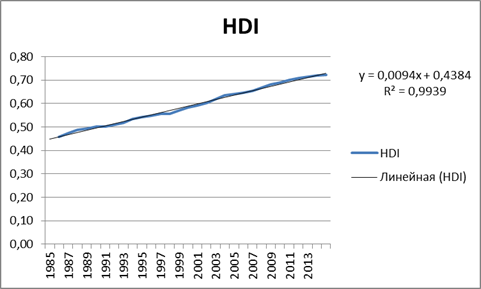
Рис. 9 Тренд показателя HDI
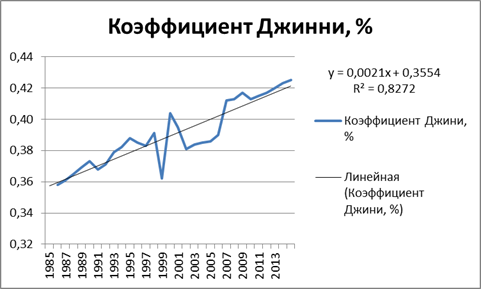
Рис. 10 Тренд показателя коэффициента Джинни
Рис. 11 Тренд показателя дефлятор ВВП
Рис. 12 Тренд показателя CPI
Рис. 13 Тренд показателя GCI
2.2. Корреляционный анализ Корреляция или корреляционная зависимость — это статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение Впервые в научный оборот термин корреляция ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века. Корреляционный анализ - метод, позволяющий обнаружить зависимость между несколькими случайными величинами. Задача корреляционного анализа – измерение тесноты связи между варьирующимися признаками, определение причинных связей и оценка факторов, оказывающих наибольшее влияние на результативный признак. Выделяют следующие виды зависимостей: • Парная корреляция – связь между двумя признаками • Частная корреляция - зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков • Множественная корреляция - зависимость результативного и двух и более факторных признаков
Рис. 14 Корреляционная зависимость между показателями Из корреляционной матрицы видно, что наиболее влияющие показатели для y1 (ВВП по ППС) являются: · HDI (x4); · Стоимость нефти на мировом рынке, долл. США/бар. (x2); · GCI (х8) Для y2 (Темп роста ВВП) нет тесной связи ни с одним из показателей. Наиболее влияющие показатели для y3 (Импорт, % в общемировом/общероссийском импорте): · Стоимость нефти на мировом рынке, долл. США/бар. (x2); · HDI (x4); · GCI (х8) · Коэффициент Джини, % (x5) Для y4 (Импорт hi-tech) нет тесной связи ни с одним из показателей.
|

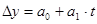






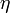 либо коэффициент корреляции
либо коэффициент корреляции 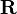 (или
(или 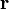 ). В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
). В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.



