Билет№12
Формула полной вероятности является следствием основных правил теории вероятностей: теорем сложения и умножения вероятностей. Допустим, что проводится некоторый опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез): { H1, H2, ¼, Hn}, Hi Ç Hj=Æ при i¹j. (3.1) Каждая гипотеза осуществляется случайным образом и представляет собой некоторые события, вероятности которых известны:
Рассматривается некоторое событие A, которое может появиться только совместно с одной из гипотез. Заданы условные вероятности события A при каждой из гипотез:
Требуется найти вероятность события A. Для этого представим событие A как сумму n несовместных событий A = (AÇH1)È(AÇH2) È... È(AÇHn). По правилу сложения вероятностей По правилу умножения вероятностей P(HiÇA)=P(Hi)×P(A/Hi). Тогда полная вероятность события A: Формула называется формулой полной вероятности. Она применяется в тех случая, когда опыт со случайным исходом распадается на два этапа: на первом “разыгрываются” условия опыта, а на втором – его результаты. Формула Байеса. Следствием правила умножения, и формулы полной вероятности является теорема гипотез или формула Байеса. По условиям опыта известно, что гипотезыН1,Н2…Нn несовместны, образуют полную группу событий:
Вероятность наступления события A совместно с гипотезой Hk определяется с использованием теоремы умножения вероятностей: P(AÇHk)=P(Hk)×P(A/Hk)=P(A)×P(Hk/A) Таким образом, можно записать:P (Hk/A) =P (Hk) ×P (A/Hk)/P (A). С использованием формулы полной вероятности Формула (3.8) называется формулой Байеса. Она позволяет пересчитывать вероятности гипотез в свете новой информации, состоящей в том, что опыт дал результат А
|

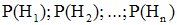
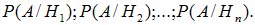

 т.е. полная вероятность события A вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при этой гипотезе.
т.е. полная вероятность события A вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при этой гипотезе.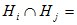 Ø при
Ø при 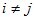 и
и  Вероятности гипотез до опыта (так называемые «априорные вероятности») известны и равны
Вероятности гипотез до опыта (так называемые «априорные вероятности») известны и равны
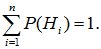 Предположим, что опыт произведен и в результате появилось событие A. Спрашивается, как нужно пересмотреть вероятность гипотез с учетом этого факта, или, другими словами, какова вероятность того, что наступлению события A предшествовала гипотеза Нк (послеопытные вероятности называются апостериорными):
Предположим, что опыт произведен и в результате появилось событие A. Спрашивается, как нужно пересмотреть вероятность гипотез с учетом этого факта, или, другими словами, какова вероятность того, что наступлению события A предшествовала гипотеза Нк (послеопытные вероятности называются апостериорными):