Дискретная случайная величина X имеет биноминальное распределение, если ее закон распределения описывается формулой Бернулли: 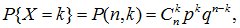 где p – параметр распределения
где p – параметр распределения 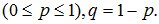 Распределение загасит от двух параметров п и р. На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из п испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в п опытах, имеет биноминальное распределение.
Распределение загасит от двух параметров п и р. На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из п испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в п опытах, имеет биноминальное распределение.
Числовые характеристики: М [Х ] = n, D[X]= npq.
Название объясняется тем, что правую часть равенства можно рассматривать как общий член разложения Бинома Ньютона:
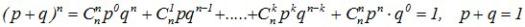 т.е.
т.е. 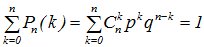
ПРОСТЕЙШИЙ ПОТОК - случайная последовательность моментов времени 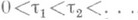 , в к-рые происходят события нек-рого потока событий (напр., потока вызовов, приходящих на телефонную станцию), удовлетворяющая условию независимости и одинаковой показательной является частным случаем процесса восстановления. С П. п. связан пуассоновский процессx(t), равный числу событий потока в отрезке времени (0, t). П. п. и соответствующий ему пуассоновский процесс удовлетворяют следующим условиям.
, в к-рые происходят события нек-рого потока событий (напр., потока вызовов, приходящих на телефонную станцию), удовлетворяющая условию независимости и одинаковой показательной является частным случаем процесса восстановления. С П. п. связан пуассоновский процессx(t), равный числу событий потока в отрезке времени (0, t). П. п. и соответствующий ему пуассоновский процесс удовлетворяют следующим условиям.
Стационарность. Для любых 0<t0, 0<t1<t2<... <tk распределение случайных величин  не зависит от t0.
не зависит от t0.
Ординарность. Вероятность появления в интервале (t, t+Dt) двух или более событий потока равна о(Dt).при 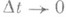 . Отсутствие последействия. При 0<t1<t2<...<tn случайные величины x(tl)-x(tl-1), l=1,..., k, независимы. Доказывается, что при выполнении этих условий и при условии
. Отсутствие последействия. При 0<t1<t2<...<tn случайные величины x(tl)-x(tl-1), l=1,..., k, независимы. Доказывается, что при выполнении этих условий и при условии
 поток будет простейшим с показательным распределением (*).
поток будет простейшим с показательным распределением (*).

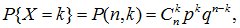 где p – параметр распределения
где p – параметр распределения 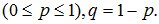 Распределение загасит от двух параметров п и р. На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из п испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в п опытах, имеет биноминальное распределение.
Распределение загасит от двух параметров п и р. На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из п испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в п опытах, имеет биноминальное распределение.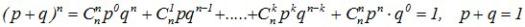 т.е.
т.е. 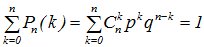
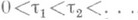 , в к-рые происходят события нек-рого потока событий (напр., потока вызовов, приходящих на телефонную станцию), удовлетворяющая условию независимости и одинаковой показательной является частным случаем процесса восстановления. С П. п. связан пуассоновский процессx(t), равный числу событий потока в отрезке времени (0, t). П. п. и соответствующий ему пуассоновский процесс удовлетворяют следующим условиям.
, в к-рые происходят события нек-рого потока событий (напр., потока вызовов, приходящих на телефонную станцию), удовлетворяющая условию независимости и одинаковой показательной является частным случаем процесса восстановления. С П. п. связан пуассоновский процессx(t), равный числу событий потока в отрезке времени (0, t). П. п. и соответствующий ему пуассоновский процесс удовлетворяют следующим условиям. не зависит от t0.
не зависит от t0.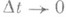 . Отсутствие последействия. При 0<t1<t2<...<tn случайные величины x(tl)-x(tl-1), l=1,..., k, независимы. Доказывается, что при выполнении этих условий и при условии
. Отсутствие последействия. При 0<t1<t2<...<tn случайные величины x(tl)-x(tl-1), l=1,..., k, независимы. Доказывается, что при выполнении этих условий и при условии поток будет простейшим с показательным распределением (*).
поток будет простейшим с показательным распределением (*).


