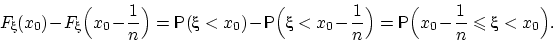Наиболее общей формой закона распределения, пригодной для всех случайных величин (как дискретных, так и недискретных) является функция распределения.
Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент функции x:
F(x)=P{X<x}.
(F1) она не убыва ет: если 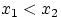 то
то  ; Доказательство свойство: для любых чисел
; Доказательство свойство: для любых чисел
X1<X2 событие  влечет событие
влечет событие 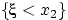 т.е
т.е  Но вероятность монотонная функция событий, поэтому
Но вероятность монотонная функция событий, поэтому 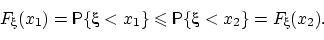
(F2) cуществуют пределы  и
и  Заметим сначала, что существование пределов в свойствах (F2), (F3) вытекает из монотонности и ограниченности функции. Остается лишь доказать равенства
Заметим сначала, что существование пределов в свойствах (F2), (F3) вытекает из монотонности и ограниченности функции. Остается лишь доказать равенства
 ,
,  и
и  Для этого в каждом случае достаточно найти предел по какой-нибудь подпоследовательности, так как существование предела влечёт совпадение всех частичных пределов Докажем, что
Для этого в каждом случае достаточно найти предел по какой-нибудь подпоследовательности, так как существование предела влечёт совпадение всех частичных пределов Докажем, что 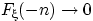 при
при 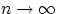 . Рассмотрим вложенную убывающую последовательность событий:
. Рассмотрим вложенную убывающую последовательность событий: 
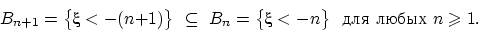 Пересечение В всех этих событий состоит из тех и только тех w, для которыхE(w) меньше любого вещественного числа. Но для любого элементарного исхода w значениеE(w) вещественно, и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение событий Bn не содержит элементарных исходов, т.е.
Пересечение В всех этих событий состоит из тех и только тех w, для которыхE(w) меньше любого вещественного числа. Но для любого элементарного исхода w значениеE(w) вещественно, и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение событий Bn не содержит элементарных исходов, т.е.  . По свойству непрерывности меры,
. По свойству непрерывности меры,
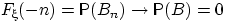 при
при 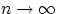
Покажем, что 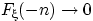 при
при 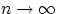 т.е
т.е  . Обозначим черезBn собитие
. Обозначим черезBn собитие  События Bn вложены:
События Bn вложены:  а пересечение B этих событий снова пусто — оно означает, что E больше любого вещественного числа. По свойству непрерывности меры,
а пересечение B этих событий снова пусто — оно означает, что E больше любого вещественного числа. По свойству непрерывности меры, 
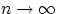 (F3) она в любой точке непрерывна слева:
(F3) она в любой точке непрерывна слева: 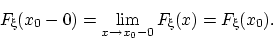
Достаточно доказать, что  при
при 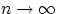 Иначе говоря, доказать сходимость к нулю следующей разности:
Иначе говоря, доказать сходимость к нулю следующей разности: 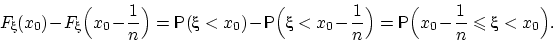

 то
то  ; Доказательство свойство: для любых чисел
; Доказательство свойство: для любых чисел влечет событие
влечет событие 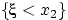 т.е
т.е  Но вероятность монотонная функция событий, поэтому
Но вероятность монотонная функция событий, поэтому 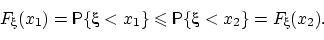
 и
и  Заметим сначала, что существование пределов в свойствах (F2), (F3) вытекает из монотонности и ограниченности функции. Остается лишь доказать равенства
Заметим сначала, что существование пределов в свойствах (F2), (F3) вытекает из монотонности и ограниченности функции. Остается лишь доказать равенства Для этого в каждом случае достаточно найти предел по какой-нибудь подпоследовательности, так как существование предела влечёт совпадение всех частичных пределов Докажем, что
Для этого в каждом случае достаточно найти предел по какой-нибудь подпоследовательности, так как существование предела влечёт совпадение всех частичных пределов Докажем, что 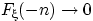 при
при 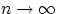 . Рассмотрим вложенную убывающую последовательность событий:
. Рассмотрим вложенную убывающую последовательность событий: 
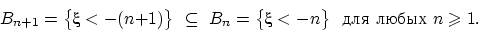 Пересечение В всех этих событий состоит из тех и только тех w, для которыхE(w) меньше любого вещественного числа. Но для любого элементарного исхода w значениеE(w) вещественно, и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение событий Bn не содержит элементарных исходов, т.е.
Пересечение В всех этих событий состоит из тех и только тех w, для которыхE(w) меньше любого вещественного числа. Но для любого элементарного исхода w значениеE(w) вещественно, и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение событий Bn не содержит элементарных исходов, т.е.  . По свойству непрерывности меры,
. По свойству непрерывности меры,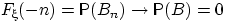 при
при  . Обозначим черезBn собитие
. Обозначим черезBn собитие  События Bn вложены:
События Bn вложены:  а пересечение B этих событий снова пусто — оно означает, что E больше любого вещественного числа. По свойству непрерывности меры,
а пересечение B этих событий снова пусто — оно означает, что E больше любого вещественного числа. По свойству непрерывности меры, 
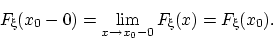
 при
при