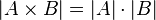Свойства. Два конечных множества равномощны тогда и только тогда, когда они состоят из одинакового числа элементов
Два конечных множества равномощны тогда и только тогда, когда они состоят из одинакового числа элементов. То есть для конечного множества понятие мощности совпадает с привычным понятием количества.Для бесконечных множеств мощность множества может совпадать с мощностью своего собственного подмножества, например Более того, множество бесконечно тогда и только тогда, когда оно содержит равномощное собственное (то есть не совпадающее с основным множеством) подмножество. Теорема Кантора гарантирует существование более мощного множества для любого данного: Множество всех подмножеств множества A имеет большую мощность, чем A, или С помощью канторова квадрата можно также доказать следующее полезное утверждение: Декартово произведение бесконечного множества A с самим собой равномощно A. Мощность декартова произведения:
Формула включения-исключения в простейшем виде:
|

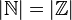 .
.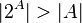 .
.