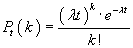Билет№21
Распределение Пуассона Пусть имеется некоторая последовательность событий, наступающих в случайные моменты времени (будем называть это потоком событий). Интенсивность потока (среднее число событий, появляющихся в единицу времени) равна λ. Пусть этот поток событий - простейший (пуассоновский), т.е. обладает тремя свойствами: 1) вероятность появления k событий за определённый промежуток времени зависит только от длины этого промежутка, но не от точки отсчёта, другими словами, интенсивность потока есть постоянная величина (свойство стационарности); 2) вероятность появления k событий в любом промежутке времени не зависит от того, появлялись события в прошлом или нет (свойство «отсутствия последействия»); 3) появление более одного события за малый промежуток времени практически невозможно (свойство ординарности). Вероятность того, что за промежуток времени t событие произойдёт k раз, равна
|