Билет№2
Дискретные вероятностные пространства. Если множество элементарных исходов конечно или счетно Важным частным случаем такого пространства является классический способ задания вероятностей, когда количество элементарных исходов конечно и все они имеют одинаковую вероятность. Тогда вероятность любого события определяется как отношение его мощности (т.е. количества элементарных исходов, благоприятствующих данному событию) к общему числу элементарных исходов:
Если А и В несовместны, то По́лной гру́ппой собы́тий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Пусть Пример Предположим, проводится подбрасывание монеты. В результате этого эксперимента обязательно произойдет одно из следующих событий: А: монета упадет орлом; В: монета упадет решкой; С: монета упадет на ребро; D: монета зависнет в воздухе. E:монету притырит подкидывающий F:монета превратится в динозавра G:монета станет летающей тарелкой Таким образом, система(А,В,С,D) является полной группой событий.
|
:, то соответствующее вероятностное пространство называется дискретным. В случае дискретных вероятностных пространств событиями обычно считают все возможные подмножества. В этом случае для задания вероятности необходимо и достаточно приписать каждому элементарному исходу число Рi так, чтобы их сумма была равна 1. Тогда вероятность любого события задается следующим образом: 
Свойсва Диск прос: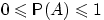
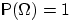
В общем случае 
Если 
то 
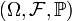есть вероятностное пространство. Любое разбиение множества 
элементами сигма-алгебры F называется полной группой событий.
