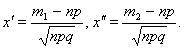Испытания наз независимыми если вероят того или иного исхода каждого из опытов независимо от того какие исходы имели др.опыты.Испытания наз.повторными если вероятности каждых отдельных опытов одинаково. Формула пуасона: Если вероятность Р наступления события А в каждом испытании постоянна и мала, а число независимых испытаний n достаточно велико, то вероятность наступления события А ровно m раз приближенно равна 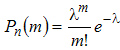 где
где 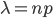 Пусть даны вероятность наступления события А в одном испытании Р и число независимых испытанийn. Обозначим
Пусть даны вероятность наступления события А в одном испытании Р и число независимых испытанийn. Обозначим 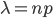 . Откуда
. Откуда 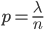 . Подставим это выражение в формулу
. Подставим это выражение в формулу 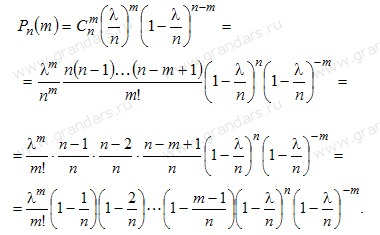 При достаточно большом!!n,, и сравнительно небольшом!!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е.
При достаточно большом!!n,, и сравнительно небольшом!!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е. 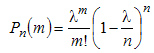 Учитывая то, что n достаточно велико, правую часть этого выражения можно рассмотреть при
Учитывая то, что n достаточно велико, правую часть этого выражения можно рассмотреть при 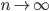 , т.е. найти предел
, т.е. найти предел 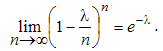 то получ нашу формулу. Локальная Му- Ла: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Рn(m)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции:
то получ нашу формулу. Локальная Му- Ла: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Рn(m)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции: 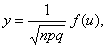 где
где 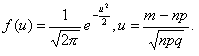 Интегральная МУ-ЛА: Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Рn(m1, m2) того, что событие А появится в п испытаниях от т1 до т2 раз. Приближенно равна определенному интегралу:
Интегральная МУ-ЛА: Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Рn(m1, m2) того, что событие А появится в п испытаниях от т1 до т2 раз. Приближенно равна определенному интегралу: 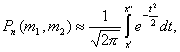 где
где 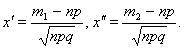

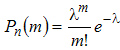 где
где 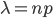 Пусть даны вероятность наступления события А в одном испытании Р и число независимых испытанийn. Обозначим
Пусть даны вероятность наступления события А в одном испытании Р и число независимых испытанийn. Обозначим 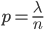 . Подставим это выражение в формулу
. Подставим это выражение в формулу 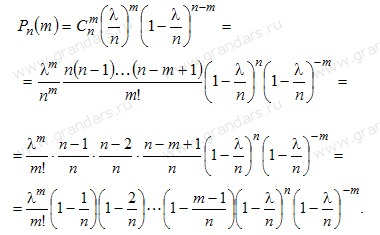 При достаточно большом!!n,, и сравнительно небольшом!!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е.
При достаточно большом!!n,, и сравнительно небольшом!!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е. 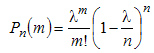 Учитывая то, что n достаточно велико, правую часть этого выражения можно рассмотреть при
Учитывая то, что n достаточно велико, правую часть этого выражения можно рассмотреть при 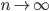 , т.е. найти предел
, т.е. найти предел 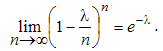 то получ нашу формулу. Локальная Му- Ла: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Рn(m)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции:
то получ нашу формулу. Локальная Му- Ла: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Рn(m)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции: 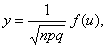 где
где 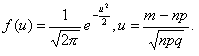 Интегральная МУ-ЛА: Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Рn(m1, m2) того, что событие А появится в п испытаниях от т1 до т2 раз. Приближенно равна определенному интегралу:
Интегральная МУ-ЛА: Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Рn(m1, m2) того, что событие А появится в п испытаниях от т1 до т2 раз. Приближенно равна определенному интегралу: 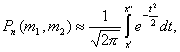 где
где