Пример 8.4.
Рассчитаем плоскую раму (рис.8.27, а) методом перемещений и выполним при этом все необходимые проверки. Последовательность расчета следующая. 1. Определение степени кинематической неопределимости Степень кинематической неопределимости определяем по формуле:
где nу - число неизвестных углов поворота, равное всегда количеству жестких узлов рамы, исключая опорные; nл - число независимых линейных перемещений узлов рамы, равное степени геометрической изменяемости шарнирной схемы рамы, полученной из заданной путем введения во все жесткие узлы, включая опорные, полных шарниров. В заданной раме nу = 1. Для определения nл вводим во все жесткие узлы, включая опорные, полные шарниры и находим степень геометрической изменяемости полученной шарнирной схемы рамы (рис.8.27, б) по формуле (8.2): nл = W = 2У – С – С0, где У = 5 - число узлов в шарнирной схеме рамы, включая и опорные; С = 4 - число стержней в шарнирной схеме рамы; Со = 5 -число опорных связей с землей шарнирной схемы рамы. nл =2×5 - 4 - 5 = 1. Полученное значение говорит о том, что шарнирная схема один раз геометрически изменяема. Действительно, под действием силы P узлы A, B и D могут переместиться влево, так как левый конец ригеля AB этой системы опирается на шарнирно-подвижную опору А, не препятствующую этому перемещению. Таким образом, заданная рама имеет одно угловое и одно линейное неизвестное перемещение, а общее количество неизвестных будет равно двум: n = ny + nл = 1 + 1 = 2. Заданная рама дважды кинематически неопределима. 2. Получение основной и эквивалентной систем метода перемещений Основную систему метода перемещений получаем путем постановки дополнительной заделки в узле В, препятствующей неизвестному угловому перемещению, и дополнительного горизонтального опорного стержня в опоре А, препятствующего неизвестному линейному перемещению (рис.8.27, в).
Рис.8.27
Загрузив основную систему внешней нагрузкой и неизвестными перемещениями Z 1 и Z 2 , равными по величине действительным перемещениям заданной системы, получим эквивалентную систему, деформирующуюся тождественно заданной (рис.8.27, г). 3. Составление канонических уравнений метода перемещений Как было указано выше, суммарная реакция в каждой дополнительно введенной связи от всех действующих в эквивалентной системе факторов равна нулю, так как эквивалентная система полностью совпадает с заданной (в которой эти связи отсутствуют) и реакций в них быть не может. В развернутом виде канонические уравнения имеют вид:
4. Вычисление коэффициентов канонических уравнений и проверка правильности их вычисления 4.1. Определение коэффициентов канонических уравнений Для определения коэффициентов необходимо построить единичные и грузовые эпюры изгибающих моментов в основной системе метода перемещений. Для их построения используются таблицы эпюр изгибающих моментов и реакций статически неопределимых балок (см. табл.8.1-8.3). Единичные и грузовые эпюры изгибающих моментов, построенные в основной системе для рассматриваемого примера, показаны на рис.8.28, а, в, д. Для определения реактивного момента r 11, возникающего в дополнительно поставленной заделке узла В от поворота этого узла на угол Z1 = 1, вырезаем узел В из эпюры M 1 (рис.8.28, б) и решаем уравнение равновесия
Реактивный момент в дополнительно поставленной заделке узла В от линейного смещения Z2 = 1 узлов В и С определяем из условия равновесия
Рис.8.28
Такая же по величине, согласно теореме о взаимности реакций, будет и реактивная сила r 21, возникающая в дополнительно поставленном горизонтальном стержне опоры А от поворота заделки узла В на угол Z1 = 1: r12 = r21 = 0,375 EJс. Реактивный момент R 1 Pq , возникающий в заделке узла В от внешних нагрузок Р и q, найдем из уравнения равновесия
Реактивное усилие r22, возникающее в горизонтальном опорном стержне опоры А от перемещения узлов В и С на величину Z2 = 1, найдем проведя разрез I-I на эпюре M 2 (см. рис.8.28, в) и определив действующие в местах сечения элементов горизонтальные усилия (рис.8.7,а) из уравнения равновесия
Рис.8.29
Проведя разрез II-II на эпюре MPq (рис.8.28, д) и определив горизонтальные усилия в рассеченных элементах, из уравнения
Определяя реактивные усилия, всегда следует иметь в виду, что они считаются положительными, если направления их действия совпадают с принятым направлением действия неизвестных перемещений Z 1 и Z 2. 4.2. Проверка правильности вычисления коэффициентов Проверка правильности вычисления главных и побочных коэффициентов канонических уравнений метода перемещений выполняется аналогично проверке коэффициентов уравнений при расчете методом сил, то есть проверяется удовлетворение равенства
Удовлетворение этого равенства свидетельствует о правильности вычисления главных и побочных коэффициентов. Таким образом, для выполнения этой проверки, называемой универсальной, необходимо построить суммарную единичную эпюру изгибающих моментов в основной системе метода перемещений Ms = M 1 + M 2 . Эта эпюра обычно строится путем сложения единичных эпюр M 1 и M 2. Для данного примера она представлена на рис.8.30, а.
Рис.8.30
Определив
видим, что равенство удовлетворяется. Таким образом, коэффициенты вычислены верно. 4.3. Проверка правильности вычисления грузовых коэффициентов Проверка правильности вычисления грузовых коэффициентов заключается в определении суммы всех найденных грузовых коэффициентов Построив эпюру
Сопрягая эпюру Ms с эпюрой
Равенство 5. Решение системы канонических уравнений и проверка правильности вычисления неизвестных Подставив найденные значения коэффициентов в канонические уравнения, получим:
Решив эту систему уравнений, находим:
Проверку правильности решения системы уравнений произведем путем подстановки найденных значений Z 1 и Z 2 в оба уравнения. В результате оба уравнения должны обратиться в тождества. Это будет свидетельствовать о правильности решения системы канонических уравнений:
Оба уравнения обратились в тождества. Следовательно, система решена верно. 6. Построение окончательной эпюры изгибающих моментов Мок для заданной системы Построение окончательной эпюры изгибающих моментов Мок для заданной системы производим на основании принципа независимости действия сил по формуле: Мок = M 1 Z 1 + M 2 Z 2 + MPq, т.е. путем сложения «исправленных» единичных эпюр М 1, М 2 и грузовой эпюры МPq , построенных в основной системе метода перемещений. Значения ординат «исправленных» эпюр M Z 1 и M Z 2 получим путем умножения ординат единичных эпюр M 1 и M 2, соответственно, на значения Z 1 и Z 2, найденные в результате решения системы канонических уравнений метода перемещений, с учетом их знака. Исправленные эпюры M 1 Z 1 и M 2 Z 2, полученные таким образом, представлены на рис.8.31, а и 8.31, б. Ординаты окончательной эпюры изгибающих моментов Мок определяем по вышеуказанной формуле в табличной форме (см. табл.8.5), предварительно приняв для этого нумерацию характерных сечений рамы и правило знаков для ординат эпюр изгибающих моментов (рис.8.30, в). В ригеле 0-2 эпюра изгибающих моментов изменяется по закону квадратной параболы, так как действует равномерно распределенная нагрузка. Поэтому в ригеле может иметь место экстремальное значение изгибающего момента. Для выяснения этого рассмотрим ригель 0-2, вырезанный из статически неопределимой рамы, на который действуют равномерно распределенная нагрузка q = 20 кН/м и опорные моменты в сечении 0: М 0 = 0 и в сечении 2: М 2 = -19,71 кН×м (рис.8.31, в).
Таблица 8.5
Аналитическое выражение изменения изгибающего момента в зависимости от текущей абсциссы z для рассматриваемого элемента имеет вид:
Для нахождения положения сечения, в котором может возникнуть экстремальное значение изгибающего момента, приравняем первую производную изгибающего момента нулю:
Определив из уравнения равновесия
Таким образом: Подставив найденное значение z0 = 1,75 м в аналитическое выражение изменения момента (8.25), определяем величину:
По найденным значениям ординат строим окончательную эпюру изгибающих моментов для заданной системы (рис.8.31, г). 7. Проверка правильности построения окончательной эпюры изгибающих моментов Мок Для того, чтобы убедиться в правильности построения эпюры Мoк, производим статическую и деформационную проверки. Для статической проверки, как и в методе сил, вырезаем незакрепленный жесткий узел В из эпюры Мoк , прикладываем действующие в нем изгибающие моменты и проверяем удовлетворение уравнения равновесия
Следовательно, узел В находится в равновесии, что свидетельствует о правильности построения эпюры Мoк. Однако, как и в методе сил, уравнения равновесия жестких незакрепленных узлов системы иногда удовлетворяются и при неправильно построенных в основной системе единичных и грузовых эпюрах, а также неправильном вычислении величин неизвестных перемещений. Поэтому для полной гарантии правильности построения эпюры Мoк сделаем деформационную проверку, физический смысл которой состоит в проверке отсутствия перемещений в сечениях заданной системы, в которых заведомо они отсутствуют. Проверим отсутствие перемещений по направлению опорного стержня опоры А заданной системы. Выбрав основную систему метода сил и приложив единичную сосредоточенную силу Х = 1 в сечении А по направлению опорного стержня, строим единичную эпюру изгибающих моментов МX =1 (рис.8.9, е) и после чего вычисляем интеграл Мора по правилу Верещагина. Сопрягая эту эпюру с эпюрой Мoк, получим:
Вертикальное перемещение сечения А отсутствует, следовательно, эпюра Мoк построена верно.
Рис.8.31
8. Построение эпюры Q по эпюре Мок Эпюру Q для заданной системе по эпюре Мoк строим, как и в методе сил, используя для определения ее ординат формулу (8.26). Учитывая принятое правило знаков при построении эпюры Мoк , обход рамы производим слева направо, начиная с опоры А и находясь все время лицом к оси каждого участка рамы. Последовательность обхода показана на рис.8.30, в пунктиром со стрелками. Участок 0-2. На этом участке действует распределенная внешняя нагрузка q = 20 кН/м и опорные моменты Мпр = М 2 = -19,71 кН×м и Млев = М 0 = 0:
Откуда, при z = 0:
a при z = 4
Участок 3-4. На этом участке нагрузка отсутствует, поэтому:
Участок 4¢-5. Аналогично:
Участок 6-7. Аналогично:
Участок 8-9. На этом участке нагрузка также отсутствует, поэтому:
По найденным ординатам строим эпюру Q для заданной рамы (рис.8.32, а).
Рис.8.32 9. Построение эпюры N для заданной рамы Ординаты эпюры N определяем из уравнений равновесия Узел D:
Узел В:
По найденным ординатам строим эпюру N (рис.8.32, б). 10. Статическая проверка рамы в целом Для выполнения этой проверки необходимо убедиться в справедливости трех уравнений равновесия Составив уравнения равновесия, проверяем их удовлетворение, т.е. обращение их в тождество:
Все уравнения обратились в тождества, следовательно, рама находится в равновесии и эпюры Q, N и Mок построены верно.
8.8. Учет продольных сил в расчетах сооружений методом перемещений
Необходимость учета продольных сил при расчете стержневых систем методом перемещений требует особого подхода к определению количества неизвестных в решаемых задачах. При этом формула (8.1) остается справедливой, т.е. по-прежнему
Число неизвестных угловых перемещений nθ остается таким же, как и в случае, когда влиянием продольных сил на конечный результат расчета мы пренебрегаем, т.е. оно равно количеству жестких узлов сооружения. В рассматриваемом случае иным становится число неизвестных линейных перемещений узлов системы nΔ, которое определяется по шарнирной схеме сооружения, образуемой теперь не только введением режущих цилиндрических шарниров в жесткие узлы, но и удалением тех элементов, где требуется учесть продольные силы.
|

 ,
,
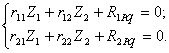
 :
: , откуда
, откуда 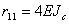 .
. .
.
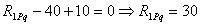 кН×м.
кН×м.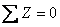 :
: .
.
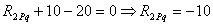 кН.
кН.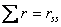 , где
, где 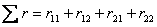 - сумма всех найденных единичных коэффициентов;
- сумма всех найденных единичных коэффициентов;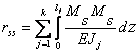 - интеграл, определяемый по правилу Верещагина, т.е. умножением суммарной единичной эпюры Ms (Ms = M 1 + M 2) на себя.
- интеграл, определяемый по правилу Верещагина, т.е. умножением суммарной единичной эпюры Ms (Ms = M 1 + M 2) на себя.
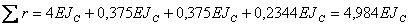 ;
;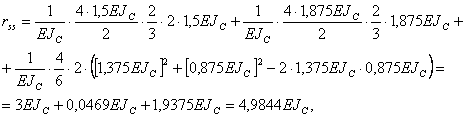
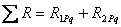 и величины
и величины  , определяемой по правилу Верещагина, т.е. сопряжением суммарной единичной эпюры
, определяемой по правилу Верещагина, т.е. сопряжением суммарной единичной эпюры  с эпюрой изгибающих моментов
с эпюрой изгибающих моментов  , построенной в основной статически определимой системе метода сил от действия только внешних нагрузок P и q. При правильном определении грузовых коэффициентов величины
, построенной в основной статически определимой системе метода сил от действия только внешних нагрузок P и q. При правильном определении грузовых коэффициентов величины 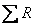 и
и 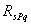 должны быть равны, т.е.
должны быть равны, т.е. 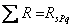 .
.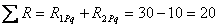 .
.
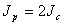 ).
).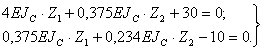
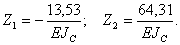
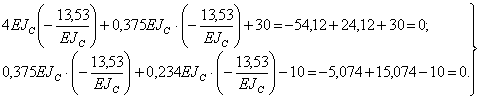
 . (8.25)
. (8.25) . (8.26)
. (8.26)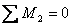 величину опорной реакции Q0 и решив (8.26), найдем z0, т.е. абсциссу сечения, где возникает экстремальное значение момента:
величину опорной реакции Q0 и решив (8.26), найдем z0, т.е. абсциссу сечения, где возникает экстремальное значение момента: ;
;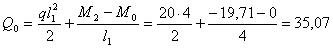 кН;
кН;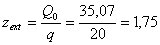 м.
м.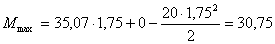 кН×м.
кН×м. .
.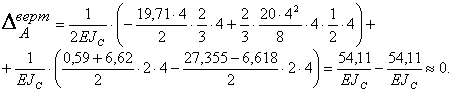
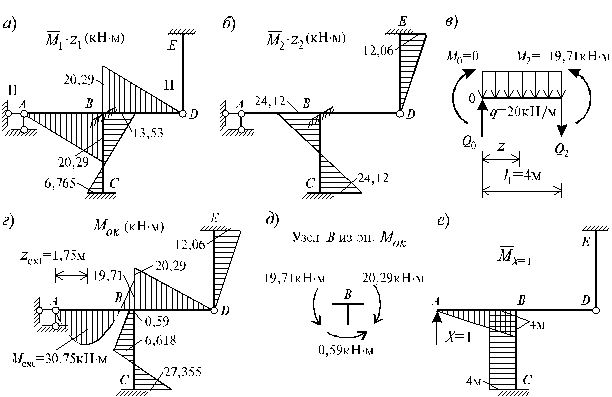
 , где 0 £ z £ l 1 = 4 м.
, где 0 £ z £ l 1 = 4 м. кН,
кН, кН.
кН. кН.
кН.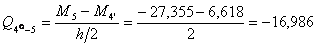 кН.
кН. кН.
кН.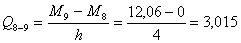 кН.
кН.
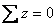 и
и  вырезанных из эпюры Q узлов рамы. К вырезанным узлам прикладываем действующие в них поперечные силы Q и искомые продольные силы N, составляем уравнения равновесия узлов и решив их, вычисляем ординаты эпюры N. При этом нормальные силы направляем от узла, предполагая, что все элементы рамы растянуты, а направление поперечных сил принимаем согласно следующему правилу: если поперечная сила положительная, то она должна вращать узел по ходу часовой стрелки, а если отрицательная - то против хода часовой стрелки.
вырезанных из эпюры Q узлов рамы. К вырезанным узлам прикладываем действующие в них поперечные силы Q и искомые продольные силы N, составляем уравнения равновесия узлов и решив их, вычисляем ординаты эпюры N. При этом нормальные силы направляем от узла, предполагая, что все элементы рамы растянуты, а направление поперечных сил принимаем согласно следующему правилу: если поперечная сила положительная, то она должна вращать узел по ходу часовой стрелки, а если отрицательная - то против хода часовой стрелки.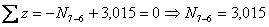 кН (растяжение);
кН (растяжение);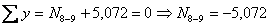 кН (сжатие).
кН (сжатие).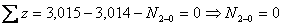 ;
;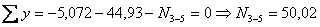 кН (сжатие).
кН (сжатие).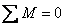 для любой отсеченной части рамы. Отсечем заданную раму от всех опор и приложим в местах сечений действующие в них силовые факторы, величины и направления которых берем из эпюр Mок, Q и N (рис.8.32, в).
для любой отсеченной части рамы. Отсечем заданную раму от всех опор и приложим в местах сечений действующие в них силовые факторы, величины и направления которых берем из эпюр Mок, Q и N (рис.8.32, в).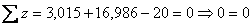 ;
;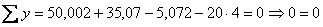 ;
;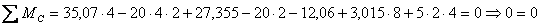 .
. .
.


