1 страница. <question>Мынаны ақиқат оқиға деп атайды:
Блок <question> Мынаны ақиқат оқиға деп атайды: <variant> әрбір сынақ нәтижесінде орындалатын оқиға; <variant> әрбір, ықтималдығы 0-ге тең оқиға; <variant> әрбір, ықтималдығы 1-ден артық оқиға; <variant> сынақтың ешбір нәтижесінде орындалмайтын оқиға; <variant> дұрыс жауап көрсетілмеген;
<question> Ақиқат оқиғаның ықтималдығы мынаған тең: <variant> 1; <variant> <variant> <variant> 0; <variant> 2/3; <question> Мынаны жалған оқиға деп атайды: <variant> сынақтың ешбір нәтижесінде орындалмайтын оқиға; <variant> әрбір сынақ нәтижесінде орындалатын оқиға; <variant> әрбір ықтималдығы 1-ге тең оқиға; <variant> әрбір ықтималдығы 1-ден артық оқиға; <variant> дұрыс жауап көрсетілмеген;
<question> Жалған оқиғаның ықтималдығы мынаған тең: <variant> 0; <variant> <variant> <variant> 1; <variant> -1;
<question> Лапластың локальды формуласын көрсетіңіздер: <variant> <variant> <variant> <variant> <variant>
<question> Байес формуласын көрсетіңіз, <variant> <variant> <variant> <variant> <variant>
<question> <variant> Бернулли <variant> Лагранж <variant> Лаплас <variant> Пуассон <variant> Байес
<question> Қолдағы 5 папканы араластырып жіберіп неше әдіспен үшеуден әртүрлі папка алуға болады: <variant> 10 <variant> <variant> 15 <variant> 8 <variant> 4
<question> Егер топта 9 студент болса, онда құрамында 3 ден топ активін неше әдістен құруға болады: <variant> 504 <variant> 32. <variant> 36. <variant> 120. <variant> 84. <question> 1-ден 35-ке дейінгі бүтін сандар арқылы нөмірленген 35 емтихан билеттерінің ішінен қалай болса солай бір билет алынған. Суырылған билеттің нөмірі үшке еселі сан болу ықтималдығы қандай? <variant> <variant> <variant> <variant> <variant> <question> Топта 6 жігіт және 18 қыз бар. Театрға бару үшін бір билет жеребиге салынған. Билетті қыздың алу ықтималдығы қандай? <variant> 0,75. <variant> 0,65. <variant> 0,55. <variant> 0,45. <variant> 0,85. <question> Онбес жігіттен және бес қыздан тұратын туристер тобы жеребе тастай, төрт адамнан тұратын шаруашылық командасын сайлаған. Осы команданың құрамында екі жігіт пен екі қыздың болу ықтималдығы қандай? <variant> 0,217. <variant> 0,317. <variant> 0,117. <variant> 0,017. <variant> 0,517. <question> Бірдей алты карточкеде А,А,Ы,Т,Л,М әріптері жазылған. Оларды жақсылап араластырып, содан кейін бір-бірден алып, бір қатарға қойғанда АЛМАТЫ сөзінің шығу ықтималдығы қандай? <variant> <variant> <variant> <variant> <variant> <question> 1000 жаңа туған баланың 517-сі ұл болды. Ұл баланың туу жиілігі қандай? <variant> 0,517. <variant> 0,417. <variant> 0,317. <variant> 0,617. <variant> 0,718. <question> Бір жылда екі фирманың банкрот болу ықтималдығы 0,06 және 0,09. Жылдың аяғында екі фирманың жұмыс істеп туру ықтималдығын тап: <variant> 0,8500. <variant> 0,8146. <variant> 0,0546. <variant> 0,0054. <variant> 1. <question> Топтағы 15 студенттің 10-спортшы. Кез келген шақырылған бір студенттің спортшы екендігінің ықтимамлдығын табыңыз: <variant> <variant> <variant> <variant> <variant> <question> Нысанаға тигізу ықтималдығы 0,8. Нысанаға тигізе алмау ықтималдығын табыңыз: <variant> 0,2. <variant> 0,02. <variant> 1. <variant> 0,1. <variant> 0,8. <question> Ойын сүйегі лақтырылады. Жұп ұпайлар түсу ықтималдығын табыңыз: <variant> <variant> <variant> <variant> <variant> <question> 10 лотерея билетінің ішінде 3 ұтыс билеті бар. Алынған кез келген 2 билеттің екеуіне де ұтыс шығу ықтималдылығын табыңыз. <variant> <variant> <variant> <variant> <variant> <question> Ойын сүйегі лақтырылды. Үштен артық ұпай түсу ықтималдығын табыңыз: <variant> 1/2. <variant> 1/6. <variant> 5/6. <variant> 1/3. <variant> 2/3. <question> Нүктенің пропорционал облыстарға түсу ық тималдығының формуласы: <variant> <variant> <variant> <variant> 0 <variant> 1 <question> Нүктенің кеңістіктегі пропорционал фигураларға түсу ықөтималдығының формуласы <variant> <variant> <variant> <variant> 0 <variant> 1 <question> Кез- келген екі таңбалы санның 5-ке бөлінетіндігі ықтималдығын табызыз. <variant> <variant> <variant> <variant> <variant> <question> Мынау кiмнiң формуласы:
<variant> Лапластың <variant> Байестің <variant> Бернулли <variant> Пуассон <variant> Лагранж <question> Мынау кiмнiң формуласы:
<variant> Байес <variant> Бернулли <variant> Пуассон <variant> Лагранж <variant> Лаплас <question> «Ойын сүйегін бір рет лақтырғанда 5 ұпайы түсті» деген оқиға: <variant> кездейсоқ <variant> мүмкін емес <variant> ақиқат <variant> үйлесімді <variant> дұрыс жауабы жоқ. <question> W=m/n қатынасы: <variant> Салыстырмалы жиілік; <variant> Салыстырмалы теория; <variant> Салыстырмалы белгіОтносительной чертой; <variant> Ықтималдық жиілік; <variant> Ықтималдық теориядеп аталады. <question> Ықтималдықтар теориясы: <variant> кездейсоқ құбылыстардың заңдылығын зерттейтін математикалық ілім <variant> мүмкін емес оқиғалардың ықтималдығын зерттейді <variant> жалғыз мүмкіндікті оқиғаларды зерттейтін ілім <variant> көп өлшемді бақылау <variant> дұрыс жауабы жоқ <question> А және В оқиғалардың айырымы... деп белгiленедi <variant> А / В <variant> АÇВ <variant> АÈВ <variant> Æ <variant> А±В <question> А және В оқиғалардың қосындысы... деп белгiленедi <variant> АÈВ <variant> А / В <variant> АÇВ <variant> Æ <variant> А±В <question> А және В оқиғалардың көбейтiндiсi... деп белгiленедi <variant> АÇВ <variant> А / В <variant> Æ <variant> А±В <variant> АÈВ
<question1> <variant> Комбинаторикалық теру <variant> Теру формуласы <variant> Орналастыру формуласы <variant> Стирлинг формуласы <question1> <variant> Теру формуласы <variant> Комбинаторикалық теру <variant> Орналастыру <variant> Стирлинг <question1> <variant> Орналастыру <variant> Комбинаторикалық теру <variant> Теру қасиеті <variant> Стирлинг формуласы <question1> <variant> Теру қасиеті <variant> Теру формуласы <variant> Орналастыру формуласы <variant> Стирлинг формуласы <question1> <variant> Теру қасиеті <variant> Теру формуласы <variant> Орналастыру формуласы <variant> Стирлинг формуласы <question1> <variant> n - дәрежелі Нютон биномының соңғы коэффициенті <variant> Теру формуласы <variant> Орналастыру <variant> Стирлинг формуласы
<question1> <variant> Стирлинг формуласы <variant> Теру <variant> Орналастыру формуласы <variant> n - дәрежелі Нютон биномының соңғы коэффициенті <question1> <variant> А оқиғасының салыстырмалы жиілігі <variant> Қарама - қарсы оқиғаның ықтималдығы <variant> Х үздіксіз кездейсоқ шаманың математикалық күтімі <variant> Кездейсоқ шаманың орташа квадраттық ауытқуы
<question1> <variant> Қарама - қарсы оқиғаның ықтималдығы <variant> А оқиғасының салыстырмалы жиілігі <variant> Х үздіксіз кездейсоқ шаманың математикалық күтімі <variant> Кездейсоқ шаманың орташа квадраттық ауытқуы
<question1>
<variant> Толық ықтималдық формуласы. <variant> А оқиғасының салыстырмалы жиілігі <variant> Х үздіксіз кездейсоқ шаманың математикалық күтімі <variant> Қарама - қарсы оқиғаның ықтималдығы <question1> Біреуінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертпесе? <variant> Екі оқиға үйлесімсіз оқиғалар деп аталады <variant> А оқиғасының салыстырмалы жиілігі <variant> Х үздіксіз кездейсоқ шаманың математикалық күтімі <variant> Қарама - қарсы оқиғаның ықтималдығы
<question1> Егер біреуінің пайда болуы немесе болмауы екіншісінің туу ықтималдығын өзгертпесе? <variant> Екі оқиға өзара тәуелсіз оқиғалар деп аталады <variant> А оқиғасының салыстырмалы жиілігі <variant> Х үздіксіз кездейсоқ шаманың математикалық күтімі <variant> Қарама - қарсы оқиғаның ықтималдығы
<question1> [0;1] қандай аралық? <variant> Оқиғаның туу ықтималдығы жататын аралық <variant> А мен В оқиғаларының қосындысы <variant> А2 оқиғасы пайда болып, А3 пайда болмағанда туатын оқиға <variant> А пайда болып В пайда болмағанда туатын аралық
<question1> А мен В оқиғаларының кем дегенде біреуі пайда болғанда туатын оқиғаны не деп айтамыз? <variant> А мен В оқиғаларының қосындысы <variant> А мен В оқиғасының көбейтіндісі <variant> А мен В оқиғасының азайтындысы <variant> А мен В оқиғасының бөліндісі <question1> А мен В оқиғаларының екеуі бірдей пайда болғанда туатын оқиғаны не деп айтамыз? <variant> А мен В оқиғасының көбейтіндісі <variant> А мен В оқиғаларының қосындысы <variant> А мен В оқиғасының азайтындысы <variant> А мен В оқиғасының бөліндісі
<question1> Пайда болуы да болмауы да мүмкін болса? <variant> Оқиға кездейсоқ деп аталады <variant> оқиғалар үйлесімсіз деп аталады <variant> оқиғалар үйлесімді деп аталады <variant> оқиға тәуелсіз деп аталады <question1> Біреуінің пайда болуы басқасының пайда болу ықтималдығына әсер етпесе? <variant> оқиғалар үйлесімсіз деп аталады <variant> оқиғалар үйлесімді деп аталады <variant> Оқиға кездейсоқ деп аталады <variant> оқиға тәуелсіз деп аталады <question1> Біреуінің пайда болуы басқасының пайда болу ықтималдығына әсер етеді? <variant> оқиғалар үйлесімді деп аталады <variant> оқиғалар үйлесімсіз деп аталады <variant> Оқиға кездейсоқ деп аталады <variant> оқиға тәуелсіз деп аталады <question1> Біреуінің пайда болуы екінішісінің пайда болу ықтималдығын өзгертпесе? <variant> оқиға тәуелсіз деп аталады <variant> оқиғалар үйлесімсіз деп аталады <variant> Оқиға кездейсоқ деп аталады <variant> оқиғалар үйлесімді деп аталады <question1> Есептеңіз <variant> 7/4 <variant> 1/7 <variant> <variant> 0,5 <question1> Есептеңіз <variant> 12 <variant> 1 <variant> 1/3 <variant> 11 <question1> Есептеңіз: <variant> 35 <variant> 1 <variant> 1/3 <variant> 11 <question1> Есептеңіз: <variant> 110 <variant> 22 <variant> 1/3 <variant> 44 <question1> Р5 – Р3 айырымын есептеңіз. <variant> 114 <variant> 0 <variant> 289 <variant> 44 <question1> <variant> 0.5 <variant> -2 <variant> 10 <variant> 2,5
<question1> <variant> 6 <variant> 0 <variant> 5 <variant> 9 <question1> <variant> 60 <variant> 0 <variant> 3 <variant> 5 <question1> <variant> 42 <variant> 13 <variant> 3 <variant> 5
<question1>
<variant> 3 <variant> 0 <variant> 4 <variant> 5
<question1>
<variant> 1.5 <variant> 0 <variant> 4 <variant> 5 <question1> <variant> 6 <variant> 0 <variant> 4 <variant> 5 <question1> <variant> 12 <variant> 0 <variant> 4 <variant> 5 <question1> <variant> 2.1 <variant> -6 <variant> 4 <variant> 11 <question1> <variant> 2.1 <variant> -6 <variant> 4 <variant> 11 <question1> n элементтен m1 және m2-ден жасалған қайталамалы алмастыру формуласын көрсетіңіз. <variant> Pn(m1,m2)=n!/(m1!m2!)
<variant> Pn(m1,m2)=(m1!m2!) <variant> Pn(m1,m2)=m! <variant> Pn(m1,m2)=m!/(m2!) <question1> Pn(K1,K2)=Ф(X")-Ф(X′) формуласы қалай аталады? <variant> Лапластың интегралды формуласы <variant> Бернулли формуласы <variant> Пирсон формуласы <variant> Пуассон формуласы
<question1> <variant> 2,3 <variant>
|

 ;
;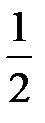 ;
;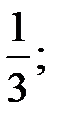

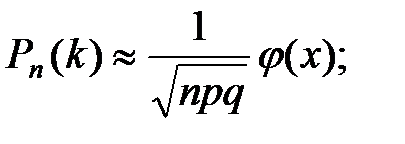
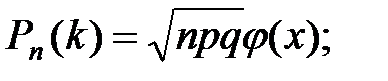
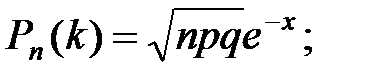

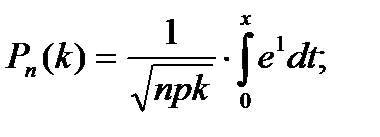
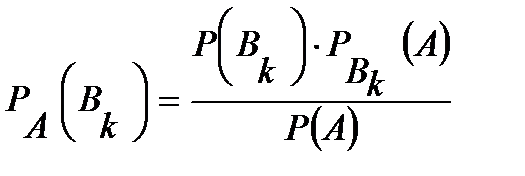
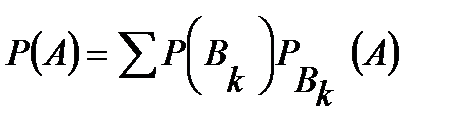
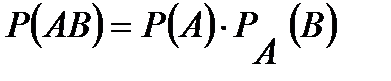

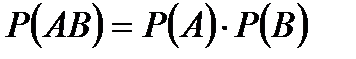
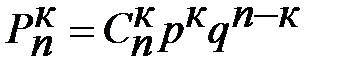 формуланың аталуы
формуланың аталуы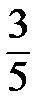

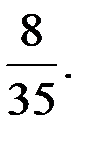
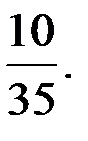
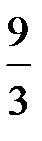
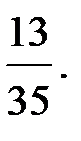
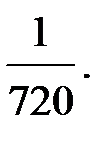





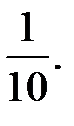
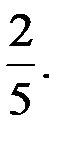

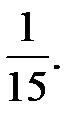

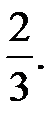

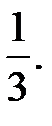


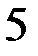
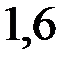




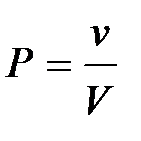

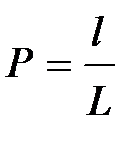




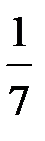


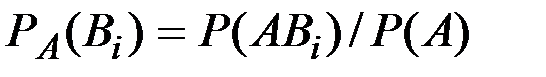


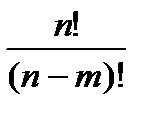
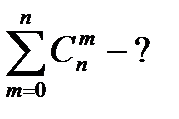
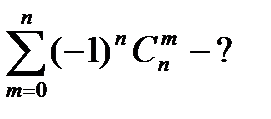
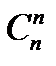
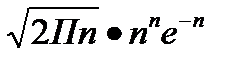
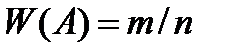 -?
-?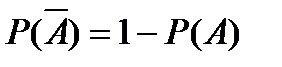
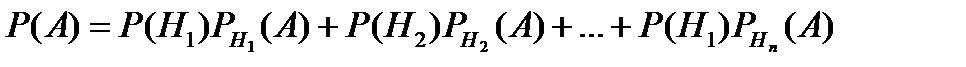 -?
-?

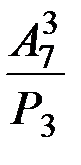 .
. .
. - есептеңіз
- есептеңіз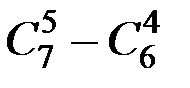 - айырымын есептеңіз.
- айырымын есептеңіз. есептеңіз.
есептеңіз.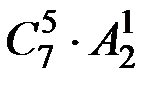 - есептеңіз
- есептеңіз - есептеңіз.
- есептеңіз.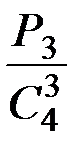 - есептеңіз.
- есептеңіз. айырымын есептеңіз.
айырымын есептеңіз.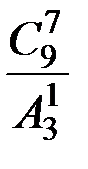 - есептеңіз
- есептеңіз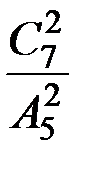 - есептеңіз.
- есептеңіз.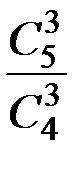 - есептеңіз
- есептеңіз теңдеуін шешіңіз
теңдеуін шешіңіз


