3 страница. Келесі оқиғалар алгебрасының қайсы теңдіктері дұрыс?
В,С <variant> В <question1> Келесі оқиғалар алгебрасының қайсы теңдіктері дұрыс? X+ X+VX=X
<variant> А,В <variant> А,С <variant> В,С <variant> А <variant> С <question1>
<variant> А оқиғасының n сынауда дәл к рет пайда болу ықтималдығы <variant> Жүргізілген өзара тәуелсіз барлық сынаулар саны <variant> Пайда болуы тиісті оқиғалар саны <variant> Әрбір сынаудағы А оқиғасының пайда болу ықтималдығы <variant> А оқиғасының к сынауда дәл n рет пайда болу ықтималдығы <question1>
<variant> Теңдеудің шешімі жоқ <variant> <variant> <variant> <variant> <question1> P(A+B)= 0 қандай А және В оқиғалары үшін орындалады. <variant> А және В мүмкін емес оқиға болғанда <variant> А мен В оқиғаларының кешенді біреуі мүмкін емес оқиға болғанда <variant> А мен В оқиғаларының кешенді біреуі ақиқат оқиға болғанда. <variant> А мен В өзара қарама - қарсы оқиғалар болғанда. <variant> Ешқандай да А және В оқиғасы үшін орындалмайды. <question1> Pn (K) ≈ <variant> Жүргізілген барлық өзара тәуелсіз сынаулар саны. <variant> Пайда болу тиісті барлық сынаулар саны. <variant> λ = nр. <variant> 2.718. <variant> Қолайлы жағдайлар саны. <question1> Нысанаға үш атқыш бір - бірден ақ атады. 1-ші атқыштың нысанаға тигізу ықтималдығы P1= 0,7, екіншісінікі P2=0,6, үшіншісінікі P3=0,8 болсын. Нысанаға тек 1 ші атқыштың оғының тиу ықтималдығы неге тең. <variant> 0.036. <variant> 0.096. <variant> 0.084. <variant> 0.056 <variant> 0.04 <question1> Екі ойын кубогы тасталды делік. Сонда көрінген ұпайлардың қосындысының 3 ке тең бөлу ықтималдығы неге тең? <variant>
<variant>
<variant>
<variant>
<variant>
<question1> А мен В өзара үилесіисіз оқиға болса, А-В қандай оқиға. <variant> А пайда болып, В пайда болмағанда туатын оқиға <variant> В пайда болып, А пайда болмағанда туатын оқиға <variant> А мен В оқиғаларының екеуі бірдей пайда болмағанда туатын оқиға <variant> В пайда болғанда туатын оқиға <variant> А пайда болғанда туатын оқиға <question1>
<variant> n элементтен к-дан жасалған қайтарымсыз терулер санын анықтайтын формула <variant> n элементтен к-дан жасалған қайталамалы терулер санын анықтайтын формула. <variant> n элементтен к-дан жасалған қайталамалы орналастырулар санын анықтайтын формула. <variant> n элементтен к-дан жасалған қайталамалы аргументтер санын анықтайтын формула. <variant> n элементтен к-дан жасалған қайталамалы функциялар санын анықтайтын формула. <question1> n элементі А жиынның m элементті (m<n) қанша ішкі жиыны бар. <variant>
<variant>
<variant>
<variant>
<variant> Р= n <question1> B = {1.2.3.4} жиыны берілген. A42 неге тең? <variant> <variant> <variant> <variant> <variant> <question1>
<variant> 10, 20 және 120 <variant> 10, 120 және 20 <variant> 120, 10 және 20 <variant> 10, 10 және 30 <variant> 12, 10 және 25 <question1> Тиын тасталды. Осы құбылыста сынау (тәжірибе) қайсы, оқиға қайсы? <variant> Тиынның тасталу - сынау, оның цифр (елтаңба) жағымен түсуі - оқиға <variant> Екеуіде сынау <variant> Тиынның тасталуы - оқиға, оның цифр (елтаңба) жағымен түсуі - сынау <variant> Бұл қимылдарда сынауда, оқиғада жоқ. <variant> Екеуіде оқиға. <question1> 1-ден 30-ға деінгі сандар берілген. Осылардың арасынан кездейсоқ алынған санның 30-дың бөлгіші болу ықтималдығы неге тең? <variant>
<variant> 0.5 <variant> 0.6 <variant> 1.5 <variant> 1/9 <question1> P(A+B) = P(A)+P(B)-P(AB) формуласы қандай екі А және В оқиғаларының ықтималдығын табуға қолданылады. <variant> Үйлесімді. <variant> Кез-келген <variant> Тәуелсіз <variant> Қарама-қарсы <variant> Тәуелді. <question1> P(A+B) = P(A) + P(B) формуласы қандай екі А және В оқиғалары үшін орындалады. <variant> А мен В үйлесімсіз оқиғалар болса <variant> Кез-келген оқиғалар болса. <variant> А және В өзара тәуелді оқиғалар болса <variant> А және В оқиғалары қарама - қарсы болса <variant> А және В өзара үйлесімді оқиғалар болса <question1> Қандай екі оқиға үлесімсіз оқиғалар деп аталады? <variant> Егер біреуінің пайда болуы, екіншісінің пайда болуын өзгертпесе <variant> Егер екеінің бірдей пайда болу мүмкін болса <variant> Біреуінің пайда болуы екіншісінің пайда болмауын тудыратын болса <variant> Егер біреуінің пайда болмауы, екіншісінің пайда болмауын тудыратын болса <variant> Егер біреуінің пайда болуы, барлығының пайда болмауын тудыратын болса <question1> Оқиғаның туу ықтималдығы жататын аралықты көрсет. <variant> [0;1] <variant> [- <variant> [0.1[ <variant> [0:+ <variant> ]- <question1> А мен В оқиғасының кобеитіндісі деп қандай оқиғаны айтамыз? <variant> А мен В оқиғаларының екеуі - бірдей пайда болғанда туатын оқиғаны айтамыз. <variant> А мен В оқиғаларының біреуі пайда болғанда туатын оқиғаны айтамыз <variant> А мен В оқиғларының кем дегенде біреуі пайда болғанда туатын оқиғаны айтамыз <variant> А пайда болып В пайда болмағанда туатын оқиғаны айтамыз <variant> А пайда болып В пайда болмағандағы оқиғаны айтамыз <question1> Келесі оқиғалардың қайсылары ақиқат оқиға? А-үш рет атқанда нысанаға үш оқтың да тиюі. Б-ойын тасын екі рет тастағанда көрінген ұпайлардың 12-ден көп болмауы. В-үш таңбалы натурал санның 1000-нан кем болуы <variant> Б,В <variant> А,Б <variant> А,В <variant> А <variant> А,Б,В <question1> Келесі оқиғалардың қайсылары мүмкін емес оқиға? А-үш ойын тасын тастағанда көрінген ұпайлардың қосындысының 19-ға тең болуы. Б-сенбі күндері Алматы журдек поездының станцияға кешігіп келуі. В-тиынды тастағанда елтаңба жағымен тусуі. <variant> А <variant> А,Б <variant> Б,В <variant> А,В <variant> Б <question1> Келесі оқиғалардың қайсылары кездейсоқ оқиға? А-ойын тасын тастағанда 5 ұпайының пайда болуы. Б-3 рет атқанда бір оқтың нысанаға тиюі. В-екі ойын тасын тастағанда көрінген ұпайлардың қосындысының 12-ден көп болуы <variant> А,Б <variant> А,В <variant> Б,В <variant> В <variant> А,Б,В <question1> Екі тиінді тастағанда елтаңба жағының кемінде бір рет көріну ықтималдығы неге тең? <variant> 0,75 <variant> 0,5 <variant> <variant> <variant> 0,25 <question1>
<variant> 10,20 және 24 <variant> 10,120 және 20 <variant> 120,12 және 20 <variant> 20,10 және 120 <variant> 20,120 және 10 <question1> Тиын тасталды. Осы құбылыста сынау (тәжірибе) қайсы, оқиға қайсы? <variant> Тиынның тасталуы - сынау, оның цифр (елтаңба) жағымен тусуі-оқиға <variant> Тиынның тасталуы - оқиға оның цифр (елтаңба) жағымен тусуі - сынау <variant> Екеуі де сынау <variant> Екеуі де оқиға <variant> Бұл қимылдарда сынау да, оқиғада жоқ <question1> Мынадай екі А және В оқиғалары үшін P(A*B) = P(A)*P(B) формуласы орындалады? <variant> Тәуелсіз <variant> Кез-келген <variant> тәуелді <variant> үйлесімді <variant> үйлесімсіз <question1> 1-ден 20-ға дейінгі сандар берілген. Осылардың арасынан кездейсоқ алынған санның 40-тың бөлгіші болу ықтималдығы неге тең? <variant> 7/20 <variant> 0,3 <variant> 0,5 <variant> <variant> 0,6 <question1> А мен В оқиғалардың кемінде біреуі пайда болғанда туатын оқиғаны қандай оқиға деп айтады? <variant> қосындысы <variant> салдары <variant> айырымы <variant> көбейтіндісі <variant> қарама-қарсысы <question1> P(A+B)=P(A)+P(B)-P(A*B) формуласы қандай екі А және В оқиғаларының ықтималдығын табуға қолданылады? <variant> тәуелді <variant> қарама - қарсы <variant> тәуелсіз <variant> үйлесімді <variant> кез-келген <question1> Қорапта 25 лотарея бар. Оның 15-не ұтыс шыққан. Сол қораптан біртіндеп кездейсоқ екі лотарея алынады. Солардың екеуінің де ұту ықтималдығы қандай? <variant> 7/20 <variant> 2/25 <variant> 3/10 <variant> 2/5 <variant> 3/7 <question1> Толық ықтималдық формуласын көрсетіңіз <variant>
<variant>
<variant>
<variant>
<variant>
<question1> Қандай екі А және В оқиғалары үшін <variant> А және В тәуелсіз оқиғалар болса <variant> А тәуелді және В тәуелсіз оқиғалар болса <variant> кез-келген А және В оқиғалары үшін <variant> А және В өзара тәуелді оқиғалар болса <variant> А оқиғасынан В оқиғасы туындайтын болса <question1> Қандай екі оқиға үйлесімсіз оқиғалар деп аталады? <variant> Біреуінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертпесе <variant> Егер екеуінінде бірдей пайда болуы мүмкін болса <variant> Егер екеуінде бірдей пайда болуы мүмкін болмаса <variant> Егер біреуінің пайда болуы екіншісінің пайда болмауын тудыратын болса <variant> Біреуінің пайда болу ықтималдығы екіншісінің пайда болу немесе бол- мауына тәуелді болса <question1> Қандай екі оқиға өзара тәуелсіз оқиғалар деп аталады? <variant> егер біреуінің пайда болуы немесе болмауы екіншісінің туу ықтималдығын өзгертпесе <variant> біреуінің пайда болуы екіншісінің пайда болуы немесе пайда болмауына әсерін тигізетін болса <variant> біреуінің пайда болуы екіншісінің пайда болуына әсерін тигізетін болса <variant> осы екі оқиға үйлесімсіз оқиға болсы <variant> біреуінің пайда болуы екіншісінің пайда болуын тудыратын болса <question1> Оқиғаның туу ықтималдығы жататын аралықты көрсет <variant> [0;1] <variant> [0; <variant> ]0;1[ <variant> ]- <variant> [- <question1> А мен В оқиғаларының қосындысы деп... <variant> А мен В оқиғаларының кем дегенде біреуі пайда болғанда туатын оқиғаны айтамыз <variant> А мен В оқиғаларының екеуі бірдей болғанда туатын оқиғаны айтамыз <variant> А мен В - ның тек қана біреуі пайда болғанда туатын оқиғаны айтамыз <variant> А пайда болып В пайда болмағанда туатын оқиғаны айтамыз <variant> Екеуі бірдей пайда болғанда туатын оқиғаны айтамыз <question1> А мен В оқиғасының көбейтіндісі деп... <variant> А мен В оқиғаларының екеуі бірдей пайда болғанда туатын оқиғаны айтамыз <variant> А мен В оқиғаларының біреуі пайда болғанда туатын оқиғаны айтамыз <variant> А мен В оқиғаларының кем дегенде біреуі пайда болғанда туатын оқиғаны айтамыз <variant> А пайда болып В пайда болмағанда туатын оқиғаны айтамыз <variant> А да В да пайда болмағанда туатын оқиғаларды айтамыз <question1> Оқиғның туу ықтималдығы мен салыстырмалы жиілігі сынаудың қандай кездерінде есептелінеді? <variant> Ықтималдық сынауға дейін салыстырмалы жиілік сынаудан соң есептелінеді <variant> Екеуі де сынаудан бұрын есептелінеді <variant> Екеуі де сынаудан соң есептелінеді <variant> Ықтималдық сынаудан соң, салыстырмалы жиілік сынауға дейін есептелінеді <variant> Екеуі де сынаудың болу, болмауына тәуелсіз есептеледі <question1> Оқиғалар жиыны қандай кластарға бөлінеді? <variant> Кездейсоқ, ақиқат және мүмкін емес оқиғалар класына <variant> Ақиқат, мүмкін емес және тәуелсіз оқиғалар класына <variant> Кездейсоқ, үйлесімсіз, тәуелсіз оқиғалар класына <variant> Мүмкін емес, ақиқат, үйлесімсіз оқиғалар класына <variant> Қарама - қарсы, ақиқат және кездейсоқ оқиғалар класына <question1> А1,А2,А3, берліген оқиғалар болсын. Сонда (А1+А/*Ā3 қандай оқиға болады? <variant> А1 мен А2 оқиғаларының кем дегенде біреуі пайда болып, А3 оқиғасы пайда болмағанда туатын оқиға <variant> А1,А2 және А3 оқиғаларының кем дегенде біреуі пайда болғанда туатын оқиға? <variant> А1,А2 оқиғасы пайда болып, А3 пайда болмағанда туатын оқиға <variant> А2 оқиғасы пайда болып, А3 пайда болмағанда туатын оқиға <variant> (А1+А/*А3 оқиғасы мүмкін емес <question1> Кітапханада әр түрлі 10 кітап бар. Олардың 5-і әрқайсысы 40 теңгеден, 3-і 20 теңгеден, 2-і 10 теңгеден тұрады. Кездейсоқ алынған бір кітаптың бағасының 20 теңгеден аспауының ықтималдығы неге тең? <variant> 0,5 <variant> 0,75 <variant> 0,75 <variant> 0,55 <variant> <question1> Студент 20 сұрақтың 15-не дайындалған. Осы студентке емтиханды тапсырып шығу үшін 1-ші болып тапсырылған қолайлы ма немесе 2-ші болып тапсырған қолайлы ма? <variant> 1-ші болып тапсырған қолайлы <variant> Екеуі бірдей қолайлы <variant> 2-ші болып тапсырған қолайлы <variant> Екеуі де қолайсыз <variant> Ең соңғы болып тапсыру қолайлы <question1> P(A1+A2+A3+…+An)=1-q1q2q3…qn формуласы арқылы қандай оқиғаның ықтималдығы есептелінеді? <variant> А1,А2,...,Аn оқиғалардың кемінде біреуінің пайда болуының <variant> А1,А2,...,Аn - copy оқиғаларының бәрінің бірдей пайда болуының <variant> А1,А2,...,Аn - оқиғаларының тек қана біреуінің пайда болуының <variant> А1,А2,...,Аn - оқиғаларының бәрінің бірдей пайда болмауының А1,А2,...,Аn - оқиғаларының кемінде біреуінің пайда болмауының <variant> А1,А2,...,Аn - оқиғаларының кемінде біреуінің пайда болмауының <question1> Ойын тасы тасталады. 6-ұпайдың көрінуі А оқиғасы, 3-ке еселі ұпайды пайда болуы В оқиғасы, тақ ұпайлардың пайда болуы - С оқиғасы болсын. Осы оқиғалардың қайсылары үйлесімді оқиғалар <variant> А және В,В және С <variant> А және С <variant> А және В <variant> В және С <variant> А және А, А және С <question1> Ықтималдықтар теориясының қандай есептерін шығару үшін P(A+B)=P(A)+P(B) формуласын қолданылады? <variant> өзара үйлесімсіз А және В оқиғаларының кемінде біреуінің пайда болу ықтималдығын табу үшін <variant> А мен В оқиғаларының екеуінің бірдей пайда болу ықтималдығын табу үшін <variant> В оқиғасы болып кеткеннен кейінгі А оқиғасының пайда болу ықтималдығын табу үшін <variant> А оқиғасы болып кеткеннен кейінгі В оқиғасының пайда болу ықтималдығын табу үшін <variant> А мен В оқиғаларының тек қана біреуінің пайда болу ықтималдығын табу үшін <question1> Өзара тәуелді А және В оқиғаларының екеуінің бірдей пайда болу ықтималдығын қайсы формула арқылы есептейміз? <variant>
|

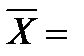 U
U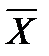 X = U
X = U Бернули формуласындағы n және к арқылы не берілген?
Бернули формуласындағы n және к арқылы не берілген?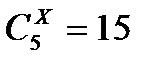 теңдеуін шешіңіз
теңдеуін шешіңіз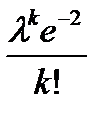 Пуассон формуласындағы n арқылы не белгіленген.
Пуассон формуласындағы n арқылы не белгіленген.

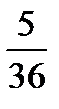
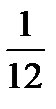

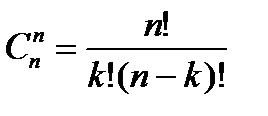 қандай формула
қандай формула
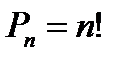
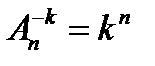
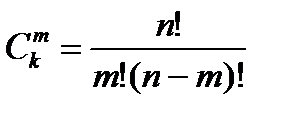
 неге тең?
неге тең?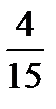
 :+
:+ 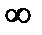 :1]
:1]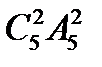 және Р4 сәйкесінше тең...
және Р4 сәйкесінше тең...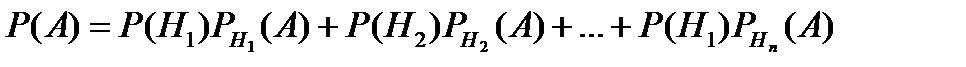
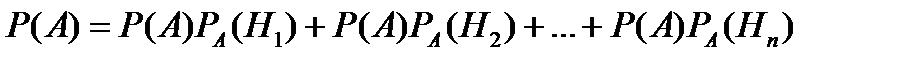
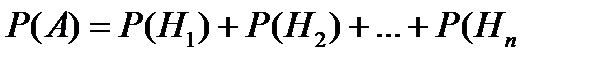
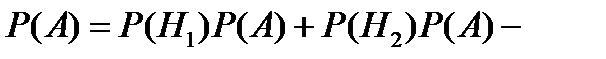

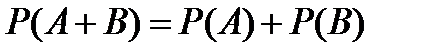 формуласы орындалады?
формуласы орындалады? [
[ ;
; 


