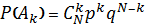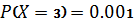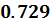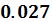Решение. Обозначим через случайную величину Х – число баз, на которых искомый товар отсутствует в данный момент
N = 3, p=0.1 Обозначим через случайную величину Х – число баз, на которых искомый товар отсутствует в данный момент. Случайная величина Х может принимать значения от 0 (товар есть на всех базах, то есть нет баз, где товара бы не было) до 3 (товара нет ни на одной из баз). Эта случайная величина распределена по биномиальному закону, и
где Аk – событие, состоящее в том, что в последовательности Nнезависимых испытаний произошло ровно k успехов, то есть из Nпосещенных баз оказались без искомого товара ровно k. Поскольку вероятность того, что товар на базе отсутствует, равна p=0.1, то вероятность того, что товар на базе естьq=1-0.1=0.9. Найдем:
Тогда закон распределения случайной величины Х в виде ряда распределения имеет вид:
Задание 6. Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно Мх, среднее квадратичное отклонение равно sx(табл. 6). Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (а, b).
|