ТЕМА 2 – Факторные модели
Целью современной теории портфеля является разработка методов, с помощью которых инвестор может выбрать оптимальный для себя портфель из бесконечного числа возможных. 1) Для решения вопроса о включении ценной бумаги в портфель инвестор оценивает ее ожидаемую доходность и стандартное отклонение, а также ковариации с другими ценными бумагами. 2) Используя такие оценки, инвестор определяет кривую эффективного множества Марковица. 3) Затем находит «касательный» портфель и определяет положение линейного эффективного множества. 4) Инвестор покупает этот «касательный» портфель и сделать заем или выдать кредит по безрисковой ставке, сумма которых зависит от предпочтений инвестора относительно соотношения риска и доходности.
Задача определения кривой эффективного множества Марковица может быть сильно упрощена с помощью оценки процесса формирования дохода (return generating process). Процессом формирования дохода называется статистическая модель, которая описывает, как образуется доход по ценной бумаге. В факторных (или индексных) моделях (factor models) предполагается, что доходность ценной бумаги реагирует на изменения различных факторов (или индексов). В модели Шарпа предполагается, что имеется только один фактор - доходность по индексу рынка. Факторная модель представляет собой попытку учесть основные экономические силы, систематически воздействующие на курсовую стоимость всех ценных бумаг. Считается, что любой аспект доходности ценной бумаги, не объясненный факторной моделью, является уникальным или специфическим для данной ценной бумаги и, следовательно, не коррелирован с уникальными аспектами доходностей других ценных бумаг. В результате факторная модель позволяет вычислить ожидаемые доходности, дисперсии и ковариации каждой ценной бумаги, а также охарактеризовать чувствительность портфеля к изменениям факторов.
2.1 Однофакторные модели
Процесс формирования дохода по ценным бумагам может быть описан одним фактором. Например, доходности ценных бумаг реагируют на предсказанный темп роста валового внутреннего продукта (ВВП). Ожидаемая доходность ценной бумаги i в период времени t: rit = ai + biFt + eit, где Ft – предсказанное значение фактора в период t, а bi – чувствительность ценной бумаги i к этому фактору. Если бы предсказанное значение фактора равнялось нулю, то доходность этой ценной бумаги составила бы а+ eit. Заметим, что eit – это случайная ошибка, т.е. это случайная переменная с нулевым математическим ожиданием и стандартным отклонением s it. Ожидаемая доходность определяется по формуле где
Дисперсия ценной бумаги i равняется: где
Ковариация ценных бумаг i и j равняется:
Уравнения дисперсии и ковариации основаны на двух предположениях 1) отсутствие корреляции случайной ошибки и фактора, то есть величина фактора совсем не влияет на величину случайной ошибки. 2) отсутствие корреляции случайных ошибок любых двух ценных бумаг, другими словами, доходности двух ценных бумаг будут меняться согласованно, только вследствие общей зависимости от изменения фактора.
Свойства однофакторных моделей. 1) Предположение о том, что доходности всех ценных бумаг реагируют на единственный общий фактор, значительно упрощает задачу определения «касательного» портфеля для заданной безрисковой ставки. Для определения его состава инвестор должен оценить все ожидаемые доходности, дисперсии и ковариации, то есть оценить аi, bi, и sеi. для любой из N рискованных ценных бумаг. Общая чувствительность ценных бумаг к фактору устраняет необходимость непосредственного вычисления ковариации между ценными бумагами. Эти ковариации уже учтены в чувствительностях ценных бумаг к фактору и в его дисперсии. 2) Второе свойство однофакторных моделей касается диверсификации. В уравнении дисперсии актива первое слагаемое
По мере того как портфель становится более диверсифицированным, доли X становятся меньше. Однако это не приведет к значительному изменению bp, поскольку эта величина является взвешенным средним чувствительностей ценных бумаг bi, в котором весами служат значения X. Диверсификация приведет к усреднению факторного риска. В то же время с увеличением диверсифицированности портфеля уменьшается нефакторный риск. Пусть в каждую ценную бумагу инвестирована одна и та же сумма, тогда Хi =1/N:
Величина внутри квадратных скобок является средним нефакторным риском для отдельных ценных бумаг. С ростом N нефакторный риск портфеля уменьшается.
Пример.
С помощью МНК данные аппроксимированы прямой линией. Эта прямая имеет положительный наклон, что указывает на существование положительной связи между скоростью прироста ВВП и доходностью акций. Более высокие темпы прироста ВВП соответствуют более высоким доходностям. Связь между предсказанным темпом прироста ВВП и доходностью акций может быть выражена в виде уравнения: rt = a + bFt + et, rt – доходность акции за период t: Ft – предсказанный темп прироста ВВП за период t; et – уникальная, или специфическая, доходность за период t; b – чувствительность к предсказанному темпу прироста ВВП; а – нулевой фактор для ВВП или доходность, которая ожидается для акций, если предсказанный темп прироста ВВП Ft =0. Однофакторная модель таким образом складывается из суммы трех элементов: 1. Элемент, одинаковый для всех периодов (член а), 2. Элемент, который меняется от периода к периоду и зависит от предсказанного 3. Элемент, специфический для конкретного рассматриваемого периода (et).
|

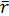 i = ai + bi
i = ai + bi  ,
,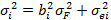
 дисперсия фактора F, a
дисперсия фактора F, a 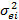 – дисперсия случайной ошибки.
– дисперсия случайной ошибки.
 называется факторным риском («рыночный», factor risk) ценной бумаги, а второе
называется факторным риском («рыночный», factor risk) ценной бумаги, а второе  ,
,